题目内容

函数f（x）=lnx+2x-1零点的个数为（ ）
A．4
B．3
C．2
D．1
【答案】分析：令函数f（x）=0，然后转化为两个简单函数图象的交点问题．
解答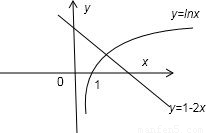：解：在同一坐标系内分别作出函数y=lnx与y=1-2x的图象，
易知两函数图象有且只有一个交点，
即函数y=lnx-1+2x只有一个零点．
故选D．
点评：本题主要考查函数零点个数的确定方法--转化为两个简单函数的图象看交点的问题．是零点判定的常用方法之一．
练习册系列答案
相关题目
已知函数f（x）=lnx-
ax
；
（Ⅰ）当a＞0时，判断f（x）在定义域上的单调性；
（Ⅱ）求f（x）在[1，e]上的最小值．
7、函数f（x）=lnx-2x+3零点的个数为（　　）
已知定义在（0，+∞）上的三个函数f（x）=lnx，g（x）=x2-af（x），h（x）=x-a
x
且g（x）在x=1处取得极值．求a的值及函数h（x）的单调递增区间．
已知函数f（x）=
lnx+kex
（k为常数，e=2.71828…是自然对数的底数），曲线y=f（x） 在点（1，f（1））处的切线与x轴平行．
（Ⅰ）求k的值；
（Ⅱ）求f（x）的单调区间；
（Ⅲ）设g（x）=（x2+x）f′（x），其中f′（x）是f（x）的导函数．证明：对任意x＞0，g（x）＜1+e-2．
已知函数f（x）=lnx-x
（1）求f（x）的单调区间；
（2）若不等式af（x）≥x-
1
2
x2在x∈（0，+∞）内恒成立，求实数a的取值范围；
（3）n∈N+，求证：
1
ln2
+
1
ln3
+…+
1
ln(n+1)
＞
n
n+1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网