题目内容
设a＞0，lga+1g
=m，则m= ．
| 5 |
| a |
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数的运算法则即可得出．
解答：
解：∵a＞0，lga+1g
=m，
∴m=lg(a×
)=lg5．
故答案为：lg5．
| 5 |
| a |
∴m=lg(a×
| 5 |
| a |
故答案为：lg5．
点评：本题考查了对数的运算法则，属于基础题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知函数f（x）=x2-cosx，对于[-
，
]上的任意x1，x2，有如下条件：①|x1|＞|x2|；②x
＞x
；
③cosx1＞cosx2；④sinx1＞sinx2．其中能使f（x1）＞f（x2）恒成立的条件序号是（ ）
| π |
| 2 |
| π |
| 2 |
2 1 |
2 2 |
③cosx1＞cosx2；④sinx1＞sinx2．其中能使f（x1）＞f（x2）恒成立的条件序号是（ ）
| A、①②③ | B、①② |
| C、①②④ | D、②③ |
F（-c，0）是双曲线
-
=1（a＞0，b＞0）的左焦点，P是抛物线y2=4cx上一点，直线FP与圆x2+y2=a2相切于点E，且PE=FE，若双曲线的焦距为2
+2，则双曲线的实轴长为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、
| ||||
B、
| ||||
| C、4 | ||||
| D、2 |
已知向量
=(2x，1)，向量
=(-4，2)，若
∥
，则
+
为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、（-2，2） |
| B、（-6，3） |
| C、（2，-1） |
| D、（6，-3） |
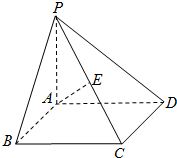如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，E是PC的中点，已知PA=AB=2，AD=2