题目内容
10.系统内有2k-1(k∈N*)个元件,每个元件正常工作的概率为p(0<p<1),若有超过一半的元件正常工作,则系统正常工作,求系统正常工作的概率pk,并讨论pk的单调性.分析 由题意,pk=$\sum_{n=0}^{k-1}$C2k-1n(1-p)np2k-1-n,利用C2k+1n=C2k-1n+2C2k-1n-1+C2k-1n-2,可得pk+1=pk+C2k-1k(1-p)kpk(2p-1),即可得出结论.
解答 解:由题意,pk=$\sum_{n=0}^{k-1}$C2k-1n(1-p)np2k-1-n,
∵C2k+1n=C2k-1n+2C2k-1n-1+C2k-1n-2,
∴pk+1=$\sum_{n=0}^{k}$C2k+1n(1-p)np2k+1-n
=$\sum_{n=0}^{k}$(C2k-1n+2C2k-1n-1+C2k-1n-2)(1-p)np2k+1-n
=$\sum_{n=0}^{k-1}$C2k-1n(1-p)np2k-1-n+C2k-1k(1-p)kpk[p-(1-p)]
=pk+C2k-1k(1-p)kpk(2p-1)
∴p>$\frac{1}{2}$,pk递增,p<$\frac{1}{2}$,pk递减,p=$\frac{1}{2}$,pk不变.
点评 本题考查概率的运用,考查学生的计算能力,确定pk+1=pk+C2k-1k(1-p)kpk(2p-1)是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若a<b<0,则下列选项正确的是( )
| A. | $\frac{b}{a}<\frac{a}{b}$ | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | an<bn(n∈N,n≥2) | D. | ?c≠0,都有ac<bc |
19.作一个平面M,使得四面体四个顶点到该平面的距离之比为2:1:1:1,则这样的平面M共能作出( )个.
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
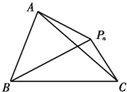 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )