题目内容
已知函数f(x)＝ax＋
－3lnx.
(1)当a＝2时，求f(x)的最小值；
(2)若f(x)在（1，e]上为单调函数，求实数a的取值范围．
解：(1)当a＝2时，f(x)＝2x＋
－3lnx，
f′(x)＝2－
－
＝
，
令f′(x)＝0，得x＝2或x＝－
(∵x>0，∴舍去负值)．
列表：
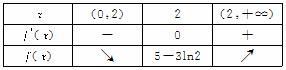
∴当a＝2时，函数f(x)的最小值为5－3ln2. .....................6分
(2)∵f′(x)＝
，
令h(x)＝ax2－3x－a，
要使f(x)在（1，e]上为单调函数，只需f′(x)在（1，e]内满足：f′(x)≥0或f′(x)≤0恒成立，只需h(x)≥0或h(x)≤0恒成立,
也就是ax2－3x－a≥0或ax2－3x－a≤0恒成立
∵x∈（1，e]
∴a≥
或 a≤恒成立.
令t= ,则 a≥ t的最大值 或 a≤t的最小值,
有单调性可求得当x∈（1，e]时，t≥
，所以t只有最小值
∴a≤
所以a≤时，f(x)在（1，e]上为单调函数．.......................12分
练习册系列答案
相关题目
(a、b为常数)，且方程f(x)－x＋12＝0有两个实根为x1＝3，x2＝4.
.
(a，b为常数，且a≠0)，满足f(2)＝1，方程f(x)＝x有唯一实数解，求函数f(x)的解析式和f[f(－4)]的值．
)