题目内容
如图所示,已知圆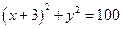 ,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足
,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足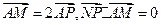 ,点N的轨迹为曲线E。
,点N的轨迹为曲线E。
(1)求曲线E的方程;
(2)求过点Q(2,1)的弦的中点的轨迹方程。
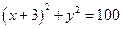 ,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足
,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足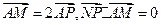 ,点N的轨迹为曲线E。
,点N的轨迹为曲线E。(1)求曲线E的方程;
(2)求过点Q(2,1)的弦的中点的轨迹方程。

(1)曲线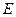 的方程为:
的方程为: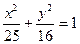
(2)中点的轨迹方程为: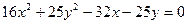
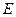 的方程为:
的方程为: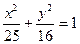
(2)中点的轨迹方程为:
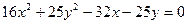
(1)∵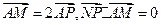
∴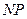 为
为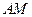 的中垂线,
的中垂线,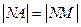 …………2分
…………2分
又因为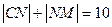 ,所以
,所以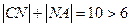
所以动点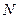 的轨迹是以点
的轨迹是以点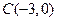 和
和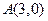 为焦点的椭圆,
为焦点的椭圆,
且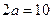 …………4分
…………4分
所以曲线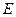 的方程为:
的方程为: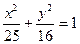 ; …………6分
; …………6分
(2)设直线与椭圆交与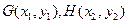 两点,中点为
两点,中点为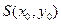
由点差法可得:弦的斜率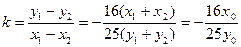 …………8分
…………8分
由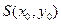 ,Q(2,1)两点可得弦的斜率为
,Q(2,1)两点可得弦的斜率为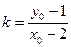 ,…………10分
,…………10分
所以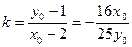 ,
,
化简可得中点的轨迹方程为: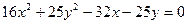 …………12分
…………12分
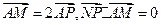
∴
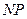 为
为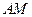 的中垂线,
的中垂线,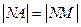 …………2分
…………2分又因为
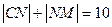 ,所以
,所以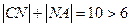
所以动点
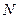 的轨迹是以点
的轨迹是以点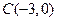 和
和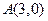 为焦点的椭圆,
为焦点的椭圆,且
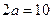 …………4分
…………4分所以曲线
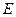 的方程为:
的方程为: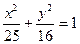 ; …………6分
; …………6分(2)设直线与椭圆交与
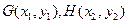 两点,中点为
两点,中点为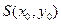
由点差法可得:弦的斜率
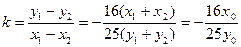 …………8分
…………8分由
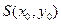 ,Q(2,1)两点可得弦的斜率为
,Q(2,1)两点可得弦的斜率为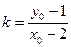 ,…………10分
,…………10分所以
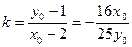 ,
,化简可得中点的轨迹方程为:
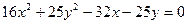 …………12分
…………12分
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
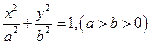 的左右焦点分别为
的左右焦点分别为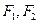 ,离心率
,离心率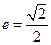 ,右准线为
,右准线为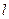 ,
,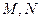 是
是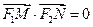 。
。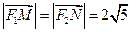 ,求
,求 的值;
的值;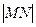 取最小值时,
取最小值时,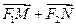 与
与 共线。
共线。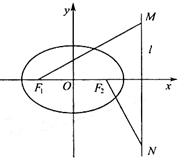
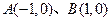 ,直线
,直线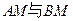 相交于点
相交于点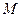 ,且它们的斜率之积为
,且它们的斜率之积为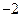 ,
,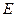 的方程;
的方程;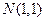 的直线
的直线 与曲线
与曲线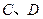 两点,且
两点,且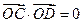 ,求直线
,求直线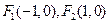 是椭圆C的两个焦点,
是椭圆C的两个焦点,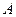 、
、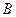 为过
为过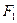 的直线与椭圆的交点,且
的直线与椭圆的交点,且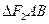 的周长为
的周长为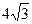 .
.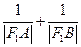 是否为定值,若是求出这个值,若不是说明理由.
是否为定值,若是求出这个值,若不是说明理由.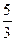 )的椭圆方程.
)的椭圆方程.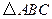 中,
中,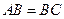 ,
,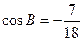 。若以
。若以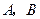 为焦点的椭圆经过点
为焦点的椭圆经过点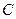 ,则该椭圆的离心率
,则该椭圆的离心率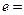 。
。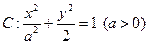 的左、右焦点分别为
的左、右焦点分别为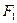 、
、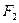 ,A是椭圆C上的一点,且
,A是椭圆C上的一点,且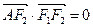 ,坐标原点O到直线
,坐标原点O到直线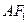 的距离为
的距离为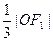 .
.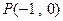 ,较y轴于点M,若
,较y轴于点M,若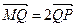 ,求直线l的方程.
,求直线l的方程.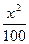 +
+ =1上的一点,F1和F2是其焦点,若∠F1PF2=60°,则△F1PF2的面积为__________________.
=1上的一点,F1和F2是其焦点,若∠F1PF2=60°,则△F1PF2的面积为__________________.