题目内容
如图，四边形ABCD为矩形，AB=| 3 |
分析：由题意知本题是一个几何概型，解决几何概型问题时，看清概率等于什么之比，试验包含的所有事件是∠BAD，而满足条件的事件是直线AP在∠CAB内时AP与BC相交时，即直线AP与线段BC有公共点，根据几何概型公式得到结果．
解答：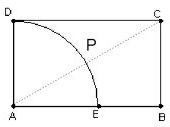
解：由题意知本题是一个几何概型，
试验包含的所有事件是∠BAD，
如图，连接AC交弧DE于P，
则tan∠CAB=
=
，
∴∠CAB=30°，
满足条件的事件是直线AP在∠CAB内时AP与BC相交时，即直线AP与线段BC有公共点
∴概率P=
=
，
故答案为：
解：由题意知本题是一个几何概型，试验包含的所有事件是∠BAD，
如图，连接AC交弧DE于P，
则tan∠CAB=
| 1 | ||
|
| ||
| 3 |
∴∠CAB=30°，
满足条件的事件是直线AP在∠CAB内时AP与BC相交时，即直线AP与线段BC有公共点
∴概率P=
3
| ||
9
|
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查了几何摡型知识，古典概型和几何概型是我们学习的两大概型，古典概型要求能够列举出所有事件和发生事件的个数，而不能列举的就是几何概型，几何概型的概率的值是通过长度、面积、和体积、的比值得到．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，A′A⊥平面ABCD．
如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=
如图，四边形ABCD为矩形，且AD=2，AB=1，PA⊥平面ABCD，PA=1，E为BC的中点．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=