题目内容
已知z，ω为复数，i为虚数单位，（1+3i）•z为纯虚数，ω=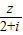
，且|ω|=5
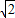，则复数ω= ．
【答案】分析：设z=a+bi（a，b∈R），利用复数的运算及（1+3i）•z=（1+3i）（a+bi）=a-3b+（3a+b）i为纯虚数，可得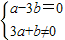
．
又ω=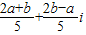
，|ω|=
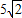，可得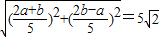
．即可得出a，b．
解答：解：设z=a+bi（a，b∈R），∵（1+3i）•z=（1+3i）（a+bi）=a-3b+（3a+b）i为纯虚数，∴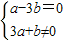
．
又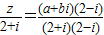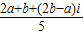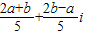ω=
=
=
，|ω|=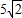
，∴
．
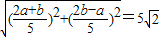把a=3b代入化为b2=25，解得b=±5，∴a=±15．
∴ω=±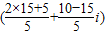
=±（7-i）．
故答案为±（7-i）．
点评：熟练掌握复数的运算法则、纯虚数的定义及其模的计算公式即可得出．
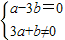．又ω=
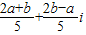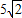，|ω|=，可得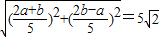．即可得出a，b．解答：解：设z=a+bi（a，b∈R），∵（1+3i）•z=（1+3i）（a+bi）=a-3b+（3a+b）i为纯虚数，∴
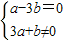．又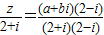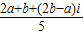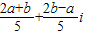ω=
==，|ω|=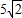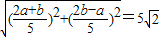，∴．把a=3b代入化为b2=25，解得b=±5，∴a=±15．
∴ω=±
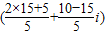=±（7-i）．故答案为±（7-i）．
点评：熟练掌握复数的运算法则、纯虚数的定义及其模的计算公式即可得出．
练习册系列答案
教材全解字词句篇系列答案
相关题目