题目内容
已知椭圆C:
+
=1的左焦点为F,过F点的直线l交椭圆于A,B两点,P为线段AB的中点,当△PFO的面积最大时,求直线l的方程.
| x2 |
| 4 |
| y2 |
| 3 |
由椭圆C:
+
=1可得a2=4,b2=3,∴c=
=1.
∴左焦点F(-1,0).
由题意只考虑直线l的斜率存在且不为0即可,
设直线l的方程为my=x+1,A(x1,y1),B(x2,y2),
联立
化为(4+3m2)y2-6my-9=0,
∴y1+y2=
,
∴yP=
=
,
∴S△PFO=
|OF|•|yP|=
=
≤
=
,当且仅当|m|=
时取等号.
此时△PFO的最大值为
,直线l的方程为±
y=x+1.
| x2 |
| 4 |
| y2 |
| 3 |
| a2-b2 |
∴左焦点F(-1,0).
由题意只考虑直线l的斜率存在且不为0即可,
设直线l的方程为my=x+1,A(x1,y1),B(x2,y2),
联立
|
∴y1+y2=
| 6m |
| 4+3m2 |
∴yP=
| y1+y2 |
| 2 |
| 3m |
| 4+3m2 |
∴S△PFO=
| 1 |
| 2 |
| |3m| |
| 2(4+3m2) |
| 3 | ||
2(
|
| 3 | ||
2×2
|
| ||
| 8 |
2
| ||
| 3 |
此时△PFO的最大值为
| ||
| 8 |
2
| ||
| 3 |

练习册系列答案
相关题目
 ,它的离心率为
,它的离心率为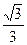 ,直线
,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.⑴求椭圆
的短半轴长为半径的圆相切.⑴求椭圆 ,左准线为
,左准线为 ,动直线
,动直线 垂直于直线
垂直于直线 ,线段
,线段 的垂直平分线交
的垂直平分线交 ,求动点
,求动点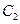 的方程;⑶将曲线
的方程;⑶将曲线 ,设曲线
,设曲线 ,焦点为
,焦点为 ,过
,过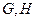 两点,过点
两点,过点 作平行于曲线
作平行于曲线 ,若
,若 ,试证明三点
,试证明三点 (
( 为坐标原点)在同一条直线上.
为坐标原点)在同一条直线上.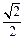 的椭圆,点F为其右焦点.
的椭圆,点F为其右焦点.
