题目内容
记关于x的不等式 的解集为P,不等式|x-1|≤3的解集为Q.
的解集为P,不等式|x-1|≤3的解集为Q.(1)若a=3,求P.
(2)若P⊆Q,求实数a的取值范围.
【答案】分析:(1)将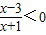 转化成(x-3)(x+1)<0进行求解即可;
转化成(x-3)(x+1)<0进行求解即可;
(2)求出集合Q,讨论a分别求出集合P,使P⊆Q,建立等量关系,求出参数a的范围,最后将符号条件的a求并集即可.
解答:解:(1)由 ,
,
转化成(x-3)(x+1)<0
解可得P={x|-1<x<3}.
(2)Q={x||x-1|≤3}={x|-2≤x≤4}.
当a>-1时,得P={x|-1<x<a},又P⊆Q,所以-1<a≤4,
当a<-1时,得P={x|a<x<-1},又P⊆Q,所以-2≤a<-1,
当a=-1时,得P=Φ,满足P⊆Q,所以,a=-1符合题意.
综上,a的取值范围是[-2,4].
点评:本题主要考查了绝对值不等式的解法,以及集合的包含关系判断及应用,属于基础题.
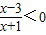 转化成(x-3)(x+1)<0进行求解即可;
转化成(x-3)(x+1)<0进行求解即可;(2)求出集合Q,讨论a分别求出集合P,使P⊆Q,建立等量关系,求出参数a的范围,最后将符号条件的a求并集即可.
解答:解:(1)由
 ,
,转化成(x-3)(x+1)<0
解可得P={x|-1<x<3}.
(2)Q={x||x-1|≤3}={x|-2≤x≤4}.
当a>-1时,得P={x|-1<x<a},又P⊆Q,所以-1<a≤4,
当a<-1时,得P={x|a<x<-1},又P⊆Q,所以-2≤a<-1,
当a=-1时,得P=Φ,满足P⊆Q,所以,a=-1符合题意.
综上,a的取值范围是[-2,4].
点评:本题主要考查了绝对值不等式的解法,以及集合的包含关系判断及应用,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 等式
等式 的解集为P, 不等式(x-1)2 ≤1的解集为Q.
的解集为P, 不等式(x-1)2 ≤1的解集为Q.  ,求P;
,求P;
 P,求正数a的取值范围.
P,求正数a的取值范围. 的解集为P,不等式
的解集为P,不等式 的解集为Q.
的解集为Q. 求正数a的取值范围
求正数a的取值范围 的解集为P, 不等式(x-1)2 ≤1的解集为Q.
的解集为P, 不等式(x-1)2 ≤1的解集为Q.  ,求P;
,求P;
 P,求正数a的取值范围.
P,求正数a的取值范围. 的解集为P,不等式|x-1|≤1的解集为Q.
的解集为P,不等式|x-1|≤1的解集为Q.