题目内容
已知椭圆C：
的离心率为
．双曲线
的渐近线与椭圆C有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C的方程为（ ）
A． | B． | C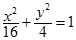． | D． |
D
解析试题分析：由椭圆C：的离心率为，得
，从而
，所以椭圆Ｃ的方程可写为：
，又因为双曲线的渐近线方程为：
与椭圆Ｃ的四个交点坐标分别为：
，从而以这四个交点为顶点的四边形的面积为
，从而
，所以椭圆C的方程为，故选Ｄ．
考点：椭圆的方程．
练习册系列答案
名校课堂系列答案
相关题目
，圆心M在二次曲线
上运动（1）若圆M与y轴相切，求圆M方程;(2) 已知圆M的圆心M在第一象限, 半径为
,动点
是圆M外一点,过点
与圆M相切的切线的长为3,求动点
，求
的取值范围？
（本小题12分）
已知椭圆C的左右焦点坐标分别是（－1，0），（1，
0），离心率
，直线
与椭圆C交于不同的两点M，N，以线段MN为直径作圆P。
（1）求椭圆C的方程；
（2）若圆P恰过坐标原点，求圆P的方程；
B.1 C.
D.
已知
是抛物线
的焦点，
是该抛物线上的两点.若线段
的中点到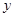
轴的距离为
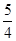，则
（ ）
| A．2 | B． | C．3 | D．4 |
已知抛物线C：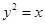
的焦点为
,
(
,
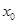)是C上一点，
=
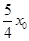，则=（ ）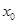
| A．1 | B．2 | C．4 | D．8 |
若双曲线
的离心率为
，则其渐近线的斜率为（ ）
A． | B． | C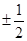． | D． |
从椭圆短轴的一个端点看长轴的两个端点的视角为
，那么此椭圆的离心率为（ ）
A． | B． | C． | D． |
若双曲线
－
＝1(a>0，b>0)上不存在点P，使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上，则该双曲线离心率的取值范围为( )
A．( ，＋∞) | B．[，＋∞) |
| C．(1，] | D．(1，) |