题目内容
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
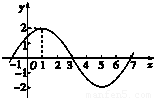
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<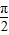 ,x∈R)的图象的一部分如图所示:
,x∈R)的图象的一部分如图所示:(1)求函数f(x)的解析式;
(2)求函数f(x)图象的对称轴方程.
【答案】分析:(1)由题图知A=2,T=8,可求得ω,又图象经过点(1,2),可求得φ,从而可求函数f(x)的解析式;
(2)由(1)知f(x)=2sin(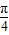 x+
x+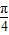 ),令
),令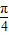 x+
x+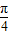 =kπ+
=kπ+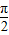 (k∈Z),即可求得函数f(x)图象的对称轴方程.
(k∈Z),即可求得函数f(x)图象的对称轴方程.
解答:解:(1)由题图知A=2,T=8,
∵T=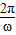 =8,
=8,
∴ω=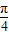 .
.
又图象经过点(1,2),
∴2sin(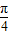 +φ)=2.
+φ)=2.
∵|φ|<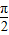 ,
,
∴φ=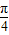 ,
,
∴f(x)=2sin(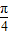 x+
x+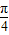 ).
).
(2)令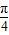 x+
x+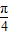 =kπ+
=kπ+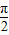 ,k∈Z.
,k∈Z.
∴x=4k+1(k∈Z).
故f(x)图象的对称轴x=4k+1(k∈Z).
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的对称性,属于中档题.
(2)由(1)知f(x)=2sin(
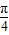 x+
x+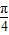 ),令
),令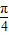 x+
x+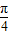 =kπ+
=kπ+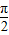 (k∈Z),即可求得函数f(x)图象的对称轴方程.
(k∈Z),即可求得函数f(x)图象的对称轴方程.解答:解:(1)由题图知A=2,T=8,
∵T=
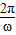 =8,
=8,∴ω=
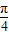 .
.又图象经过点(1,2),
∴2sin(
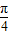 +φ)=2.
+φ)=2.∵|φ|<
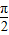 ,
,∴φ=
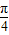 ,
,∴f(x)=2sin(
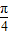 x+
x+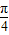 ).
).(2)令
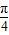 x+
x+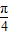 =kπ+
=kπ+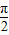 ,k∈Z.
,k∈Z.∴x=4k+1(k∈Z).
故f(x)图象的对称轴x=4k+1(k∈Z).
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的对称性,属于中档题.

练习册系列答案
相关题目