题目内容
已知函数f（x）=sin（2?x-
）（0＜?＜1）在区间[0，π]上的单调递增区间为________．
当?＜
时，增区间为[0，π]； 当?≥时，增区间为[0，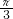
]．
分析：令 2kπ-
≤2?x-≤2kπ+，k∈z，求得函数的增区间为[
-
，+
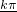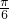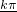]，k∈z．再由x∈[0，π]，进一步确定函数的增区间．
解答：∵函数f（x）=sin（2?x-），令 2kπ-≤2?x-≤2kπ+，k∈z，
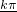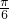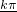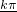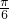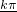求得-≤x≤+，k∈z，故函数的增区间为[-，+]，k∈z．
再由x∈[0，π]，
故当?＜时，＞π，增区间为[0，π]．
当?≥时，≤π，增区间为[0，]，
故答案为 当?＜时，增区间为[0，π]； 当?≥时，增区间为[0，]．
点评：本题主要考查由函数y=Asin（ωx+∅）的部分图象求解析式，复合三角函数的单调性，属于中档题．
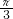时，增区间为[0，π]； 当?≥时，增区间为[0，]．分析：令 2kπ-
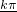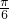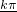≤2?x-≤2kπ+，k∈z，求得函数的增区间为[-，+]，k∈z．再由x∈[0，π]，进一步确定函数的增区间．解答：∵函数f（x）=sin（2?x-
），令 2kπ-≤2?x-≤2kπ+，k∈z，求得
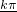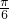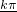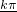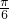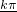-≤x≤+，k∈z，故函数的增区间为[-，+]，k∈z．再由x∈[0，π]，
故当?＜
时，＞π，增区间为[0，π]．当?≥
时，≤π，增区间为[0，]，故答案为 当?＜
时，增区间为[0，π]； 当?≥时，增区间为[0，]．点评：本题主要考查由函数y=Asin（ωx+∅）的部分图象求解析式，复合三角函数的单调性，属于中档题．
练习册系列答案
相关题目
