题目内容
已知函数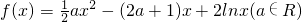 .
.
(Ⅰ)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=x2-2x,若对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求a的取值范围.
解:(Ⅰ)∵函数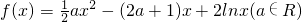 ,
,
∴ (x>0).
(x>0).
∵曲线y=f(x)在x=1和x=3处的切线互相平行,
∴f'(1)=f'(3),
即 ,
,
解得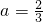 .
.
(Ⅱ) (x>0).
(x>0).
①当a≤0时,x>0,ax-1<0,
在区间(0,2)上,f'(x)>0;
在区间(2,+∞)上f'(x)<0,
故f(x)的单调递增区间是(0,2),
单调递减区间是(2,+∞).
②当 时,
时, ,
,
在区间(0,2)和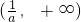 上,f'(x)>0;
上,f'(x)>0;
在区间 上f'(x)<0,
上f'(x)<0,
故f(x)的单调递增区间是(0,2)和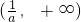 ,单调递减区间是
,单调递减区间是
③当 时,
时, ,故f(x)的单调递增区间是(0,+∞).
,故f(x)的单调递增区间是(0,+∞).
④当 时,
时,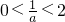 ,在区间
,在区间 和(2,+∞)上,f'(x)>0;
和(2,+∞)上,f'(x)>0;
在区间 上f'(x)<0,
上f'(x)<0,
故f(x)的单调递增区间是 和(2,+∞),单调递减区间是
和(2,+∞),单调递减区间是 .
.
(Ⅲ)由已知,在(0,2]上有f(x)max<g(x)max.
由已知,g(x)max=0,由(Ⅱ)可知,
①当 时,f(x)在(0,2]上单调递增,
时,f(x)在(0,2]上单调递增,
故f(x)max=f(2)=2a-2(2a+1)+2ln2=-2a-2+2ln2,
所以,-2a-2+2ln2<0,解得a>ln2-1,
故 .
.
②当 时,f(x)在
时,f(x)在 上单调递增,
上单调递增,
在 上单调递减,
上单调递减,
故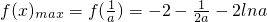 .
.
由 可知
可知 ,
,
2lna>-2,-2lna<2,
所以,-2-2lna<0,f(x)max<0,
综上所述,a>ln2-1.
分析:(Ⅰ)由函数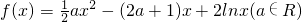 ,知
,知 (x>0).由曲线y=f(x)在x=1和x=3处的切线互相平行,能求出a的值.
(x>0).由曲线y=f(x)在x=1和x=3处的切线互相平行,能求出a的值.
(Ⅱ) (x>0).根据a的取值范围进行分类讨论能求出f(x)的单调区间.
(x>0).根据a的取值范围进行分类讨论能求出f(x)的单调区间.
(Ⅲ)对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),等价于在(0,2]上有f(x)max<g(x)max.由此能求出a的取值范围.
点评:本题考查导数在求函数的最大值与最小值问题中的综合运用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.易错点是分类不清导致致出错,解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.
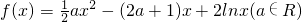 ,
,∴
 (x>0).
(x>0).∵曲线y=f(x)在x=1和x=3处的切线互相平行,
∴f'(1)=f'(3),
即
 ,
,解得
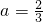 .
.(Ⅱ)
 (x>0).
(x>0).①当a≤0时,x>0,ax-1<0,
在区间(0,2)上,f'(x)>0;
在区间(2,+∞)上f'(x)<0,
故f(x)的单调递增区间是(0,2),
单调递减区间是(2,+∞).
②当
 时,
时, ,
,在区间(0,2)和
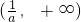 上,f'(x)>0;
上,f'(x)>0;在区间
 上f'(x)<0,
上f'(x)<0,故f(x)的单调递增区间是(0,2)和
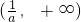 ,单调递减区间是
,单调递减区间是
③当
 时,
时, ,故f(x)的单调递增区间是(0,+∞).
,故f(x)的单调递增区间是(0,+∞).④当
 时,
时,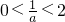 ,在区间
,在区间 和(2,+∞)上,f'(x)>0;
和(2,+∞)上,f'(x)>0;在区间
 上f'(x)<0,
上f'(x)<0,故f(x)的单调递增区间是
 和(2,+∞),单调递减区间是
和(2,+∞),单调递减区间是 .
.(Ⅲ)由已知,在(0,2]上有f(x)max<g(x)max.
由已知,g(x)max=0,由(Ⅱ)可知,
①当
 时,f(x)在(0,2]上单调递增,
时,f(x)在(0,2]上单调递增,故f(x)max=f(2)=2a-2(2a+1)+2ln2=-2a-2+2ln2,
所以,-2a-2+2ln2<0,解得a>ln2-1,
故
 .
.②当
 时,f(x)在
时,f(x)在 上单调递增,
上单调递增,在
 上单调递减,
上单调递减,故
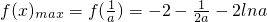 .
.由
 可知
可知 ,
,2lna>-2,-2lna<2,
所以,-2-2lna<0,f(x)max<0,
综上所述,a>ln2-1.
分析:(Ⅰ)由函数
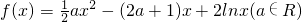 ,知
,知 (x>0).由曲线y=f(x)在x=1和x=3处的切线互相平行,能求出a的值.
(x>0).由曲线y=f(x)在x=1和x=3处的切线互相平行,能求出a的值.(Ⅱ)
 (x>0).根据a的取值范围进行分类讨论能求出f(x)的单调区间.
(x>0).根据a的取值范围进行分类讨论能求出f(x)的单调区间.(Ⅲ)对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),等价于在(0,2]上有f(x)max<g(x)max.由此能求出a的取值范围.
点评:本题考查导数在求函数的最大值与最小值问题中的综合运用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.易错点是分类不清导致致出错,解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
 -2lnx、
-2lnx、 -2lnx、
-2lnx、 -2lnx、
-2lnx、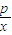 -2lnx、
-2lnx、