题目内容
圆和椭圆有很多类似的地方(形状和方程),比如椭圆
思路分析:本题主要考查椭圆和圆的联系,以及参数方程的灵活运用.要求出圆的离心率,可以根据条件求出和椭圆类似的a、b、c的值,再根据定义即可.
解:不妨设圆的方程为![]() (θ为参数),
(θ为参数),
如果看成椭圆,则在椭圆中对应的数值分别为a=b=r,所以c=![]() =0.则离心率为e=
=0.则离心率为e=![]() =0,
=0,
即把圆看成椭圆,其离心率为0,而椭圆的离心率的范围是(0,1),可见椭圆的离心率越小(接近于0),则形状就越接近于圆,离心率越大,则椭圆就越扁.

练习册系列答案
相关题目
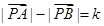 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线; 则动点P
则动点P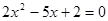 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;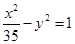 和椭圆
和椭圆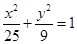 有相同的焦点.
有相同的焦点. 、
、 分别是圆
分别是圆 和椭圆
和椭圆 的弦,且弦的端点在
的弦,且弦的端点在 轴的异侧,端点
轴的异侧,端点 与
与 、
、 与
与 的横坐标分别相等,纵坐标分别同号.
的横坐标分别相等,纵坐标分别同号.
 ,且弦
,且弦 ,求直线
,求直线 ,试探究弦
,试探究弦 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;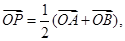 则动点P
则动点P 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率; 和椭圆
和椭圆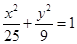 有相同的焦点.
有相同的焦点. 的左、右两个焦点.
的左、右两个焦点. )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标.
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标.