题目内容
已知函数y= 的定义域为M,
的定义域为M,
(1)求M;
(2)当x∈M时,求函数 的最大值.
的最大值.
解:(1)函数y= 有意义,故
有意义,故
可得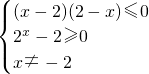 解得x∈[1,2];
解得x∈[1,2];
(2) ,令t=log2x,
,令t=log2x,
可得:g(t)=2t2+at,t∈[0,1],讨论对称轴可得:
对称轴x=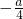 ,
,
若-
 即a≥-2,f(x)max=f(1)=a+2;
即a≥-2,f(x)max=f(1)=a+2;
若-
 即a<-2,f(x)max=f(0)=0;
即a<-2,f(x)max=f(0)=0;
∴g(t)max=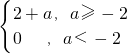 ;
;
∴函数 的最大值为:g(x)max=
的最大值为:g(x)max=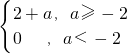
分析:(1)根据根号有意义的条件和分母不能为0,求出函数的定义域;
(2)利用换元法,t=log2x,可得g(t)=2t2+at,利用二次函数的图象和性质求出最值;
点评:此题考查函数的定义域及其求法,以及利用换元法求函数的最值问题,是一道基础题;
 有意义,故
有意义,故可得
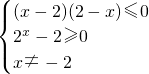 解得x∈[1,2];
解得x∈[1,2];(2)
 ,令t=log2x,
,令t=log2x,可得:g(t)=2t2+at,t∈[0,1],讨论对称轴可得:
对称轴x=
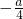 ,
,若-

 即a≥-2,f(x)max=f(1)=a+2;
即a≥-2,f(x)max=f(1)=a+2;若-

 即a<-2,f(x)max=f(0)=0;
即a<-2,f(x)max=f(0)=0;∴g(t)max=
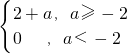 ;
;∴函数
 的最大值为:g(x)max=
的最大值为:g(x)max=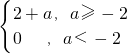
分析:(1)根据根号有意义的条件和分母不能为0,求出函数的定义域;
(2)利用换元法,t=log2x,可得g(t)=2t2+at,利用二次函数的图象和性质求出最值;
点评:此题考查函数的定义域及其求法,以及利用换元法求函数的最值问题,是一道基础题;

练习册系列答案
相关题目
 的定义域是A,函数y=
的定义域是A,函数y=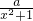 (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围. 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围. 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.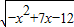 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.