题目内容
已知f(x)=x3,g(x)=-x2+x- a,若存在x0∈[-1,
a,若存在x0∈[-1, ](a>0),使得f(x0)<g(x0),则实数a的取值范围是________.
](a>0),使得f(x0)<g(x0),则实数a的取值范围是________.
0<
分析:存在x0∈[-1, ](a>0),使得f(x0)<g(x0),转化为x∈[-1,
](a>0),使得f(x0)<g(x0),转化为x∈[-1, ](a>0),使得f(x)min<g(x)max,即可.
](a>0),使得f(x)min<g(x)max,即可.
解答:由题意,存在x0∈[-1, ](a>0),使得f(x0)<g(x0),转化为x∈[-1,
](a>0),使得f(x0)<g(x0),转化为x∈[-1, ](a>0),使得f(x)min<g(x)max,
](a>0),使得f(x)min<g(x)max,
x∈[-1, ](a>0)时,f(x)=x3,单调增,∴f(x)min=-1
](a>0)时,f(x)=x3,单调增,∴f(x)min=-1
若0<
 ,即0<a
,即0<a 时,函数在区间[-1,
时,函数在区间[-1, ](a>0)上单调增,∴g(x)max=
](a>0)上单调增,∴g(x)max= =-
=-
∴-1<- ,∴
,∴ <a<
<a<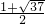 ,∴0<a
,∴0<a ;
;
当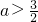 时,g(x)max=
时,g(x)max=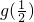 =
=
∴-1< ,∴
,∴
∴ <
<
∴0<
故答案为:0<
点评:本题考查导数知识的运用,考查函数的最值,解题的关键是存在x0∈[-1, ](a>0),使得f(x0)<g(x0),转化为x∈[-1,
](a>0),使得f(x0)<g(x0),转化为x∈[-1, ](a>0),使得f(x)min<g(x)max.
](a>0),使得f(x)min<g(x)max.

分析:存在x0∈[-1,
 ](a>0),使得f(x0)<g(x0),转化为x∈[-1,
](a>0),使得f(x0)<g(x0),转化为x∈[-1, ](a>0),使得f(x)min<g(x)max,即可.
](a>0),使得f(x)min<g(x)max,即可.解答:由题意,存在x0∈[-1,
 ](a>0),使得f(x0)<g(x0),转化为x∈[-1,
](a>0),使得f(x0)<g(x0),转化为x∈[-1, ](a>0),使得f(x)min<g(x)max,
](a>0),使得f(x)min<g(x)max,x∈[-1,
 ](a>0)时,f(x)=x3,单调增,∴f(x)min=-1
](a>0)时,f(x)=x3,单调增,∴f(x)min=-1若0<

 ,即0<a
,即0<a 时,函数在区间[-1,
时,函数在区间[-1, ](a>0)上单调增,∴g(x)max=
](a>0)上单调增,∴g(x)max= =-
=-
∴-1<-
 ,∴
,∴ <a<
<a<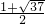 ,∴0<a
,∴0<a ;
;当
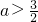 时,g(x)max=
时,g(x)max=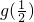 =
=
∴-1<
 ,∴
,∴
∴
 <
<
∴0<

故答案为:0<

点评:本题考查导数知识的运用,考查函数的最值,解题的关键是存在x0∈[-1,
 ](a>0),使得f(x0)<g(x0),转化为x∈[-1,
](a>0),使得f(x0)<g(x0),转化为x∈[-1, ](a>0),使得f(x)min<g(x)max.
](a>0),使得f(x)min<g(x)max. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目