Question

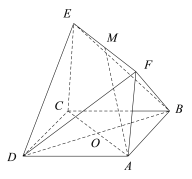
【题目】如图，已知正方形和矩形所在的平面互相垂直， ，，M是线段的中点.

（Ⅰ）求证：∥平面；

（Ⅱ）求证： 平面；

(Ⅲ) 求点到面的距离.

Answer 1

【答案】（1）见解析（2）见解析（3）

【解析】

（Ⅰ）连结BD交AC于N，连结EN，证明四边形ANEM是平行四边形，得出AM∥EN从而得出AM∥平面BDE；

（Ⅱ）设,，证明，可知，则，又 所以

又,故平面

(Ⅲ) ，可求点到面的距离.

解：（Ⅰ）连结BD交AC于N，连结EN，∥AM且EM=AM ∴ ∴AM∥EN

又因为EN平面BDE 且AM平面BDE

∴AE∥平面BDE．

（Ⅱ）设,

在矩形中四边形, ，

所以， 为正方形，,故

又正方形和矩形所在的平面互相垂直，且交线为在正方形中，故

由面面垂直的性质定理，-

又 所以

又,故平面

(Ⅲ),

-