题目内容
已知函数f(x)=aex,g(x)=lnx-lna,其中a为常数,且函数y=f(x)和y=g(x)的图象在其与两坐标轴的交点处的切线相互平行.若关于x的不等式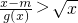 对任意不等于1的正实数都成立,则实数m的取值集合是________.
对任意不等于1的正实数都成立,则实数m的取值集合是________.
{1}
分析:利用导数的几何意义,分别求两函数在与两坐标轴的交点处的切线斜率,令其相等解方程即可得a值,不等式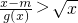 对任意不等于1的正实数都成立,即当x>1时
对任意不等于1的正实数都成立,即当x>1时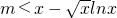 恒成立;当0<x<1时得
恒成立;当0<x<1时得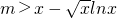 恒成立.构造新函数
恒成立.构造新函数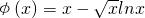 ,求其在[1,+∞)的最小值,在(0,1]上的最大值即可
,求其在[1,+∞)的最小值,在(0,1]上的最大值即可
解答:由题意可知: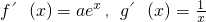 .
.
y=f(x)的图象与坐标轴交于点(0,a);y=g(x)的图象与坐标轴交于点(a,0),
∴f′(0)=g′(a).
∴ .
.
∵a>0,∴a=1
∴g(x)=lnx.
①当x>1时,由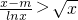 得
得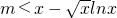 恒成立.
恒成立.
令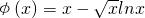 ,则
,则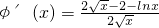 .
.
令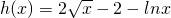 ,则
,则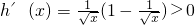 ,
,
∴h(x)在[1,+∞)上递增.
∴?x>1,h(x)>h(1)=0.
∴φ′(x)>0.
∴φ(x)在[1,+∞)上递增.
∴m≤φ(1)=1.
②当0<x<1时,由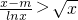 得
得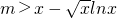 即m>φ(x)恒成立.
即m>φ(x)恒成立.
同①可得φ(x)在(0,1]上递减.
∴m≥φ(1)=1.
综合①②得m=1.
故答案为:{1}.
点评:本题综合考查了导数的几何意义及导数在解决恒成立问题、最值问题中的应用,解题时要善于构造新函数解决不等式恒成立问题,计算要认真细致.
分析:利用导数的几何意义,分别求两函数在与两坐标轴的交点处的切线斜率,令其相等解方程即可得a值,不等式
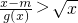 对任意不等于1的正实数都成立,即当x>1时
对任意不等于1的正实数都成立,即当x>1时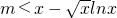 恒成立;当0<x<1时得
恒成立;当0<x<1时得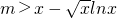 恒成立.构造新函数
恒成立.构造新函数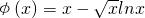 ,求其在[1,+∞)的最小值,在(0,1]上的最大值即可
,求其在[1,+∞)的最小值,在(0,1]上的最大值即可解答:由题意可知:
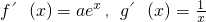 .
.y=f(x)的图象与坐标轴交于点(0,a);y=g(x)的图象与坐标轴交于点(a,0),
∴f′(0)=g′(a).
∴
 .
.∵a>0,∴a=1
∴g(x)=lnx.
①当x>1时,由
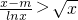 得
得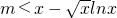 恒成立.
恒成立.令
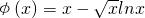 ,则
,则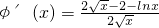 .
.令
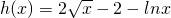 ,则
,则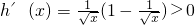 ,
,∴h(x)在[1,+∞)上递增.
∴?x>1,h(x)>h(1)=0.
∴φ′(x)>0.
∴φ(x)在[1,+∞)上递增.
∴m≤φ(1)=1.
②当0<x<1时,由
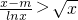 得
得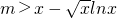 即m>φ(x)恒成立.
即m>φ(x)恒成立.同①可得φ(x)在(0,1]上递减.
∴m≥φ(1)=1.
综合①②得m=1.
故答案为:{1}.
点评:本题综合考查了导数的几何意义及导数在解决恒成立问题、最值问题中的应用,解题时要善于构造新函数解决不等式恒成立问题,计算要认真细致.

练习册系列答案
相关题目