题目内容
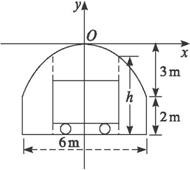
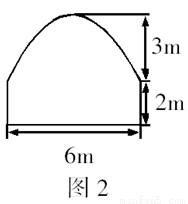
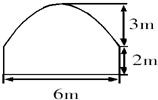 某隧道横断面由抛物线和矩形的三边组成,尺寸如图所示,某卡车载一集装箱,箱宽3m,车与箱共高4m,此车能否通过此隧道?请说明理由.
某隧道横断面由抛物线和矩形的三边组成,尺寸如图所示,某卡车载一集装箱,箱宽3m,车与箱共高4m,此车能否通过此隧道?请说明理由.
分析:取抛物线顶点为原点,水平向右为x轴正方向建立直角坐标系,设抛物线方程,把x=3代入抛物线方程求得y,取抛物线与矩形的结合点代入抛物线方程求得p,抛物线方程可求取x=
求得y,进而与隧道的高度进行比较,结果发现而者的差大于车与箱的高,判断出卡车可以通过此隧道.
| 3 |
| 2 |
解答:解:取抛物线顶点为原点,水平向右为x轴正方向建立直角坐标系,设抛物线方程为x2=-2py(p>0),
当x=3时,y=-3,即取抛物线与矩形的结合点(3,-3),
代入x2=-2py,得9=6p,则p=
,故抛物线方程为x2=-3y.
已知集装箱的宽为3m,取x=
,则y=-
x2=-
.
而隧道高为5m,5m-
m=4
m>4m.
所以,卡车可以通过此隧道.
当x=3时,y=-3,即取抛物线与矩形的结合点(3,-3),
代入x2=-2py,得9=6p,则p=
| 3 |
| 2 |
已知集装箱的宽为3m,取x=
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
而隧道高为5m,5m-
| 3 |
| 4 |
| 1 |
| 4 |
所以,卡车可以通过此隧道.
点评:本题主要考查了抛物线的应用.考查了学生结合所学知识解决实际问题的能力.

练习册系列答案
相关题目