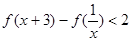题目内容
(12分)若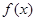 是定义在
是定义在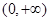 上的增函数,且对一切
上的增函数,且对一切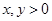 ,满足
,满足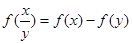 .
.
(1)求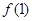 的值;
的值;
(2)若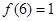 ,解不等式
,解不等式
【答案】
⑴  ⑵
⑵ 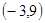
【解析】
试题分析:解(1)在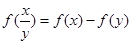 中令
中令
则有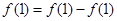 ∴
∴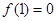
(2)∵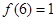 ∴
∴ ∴
∴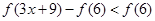 即:
即: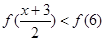 ∵
∵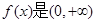 上的增函数
上的增函数
∴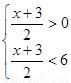 解得
解得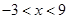 即不等式的解集为(-3,9)
即不等式的解集为(-3,9)
考点:本题主要考查赋值法以及对抽象函数单调性的考查并利用函数单调性解不等式
点评:本题已经告知函数在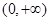 上的单调性,实质已经降低了本题的难度,本题还可不给单调性而增加条件比如:当
上的单调性,实质已经降低了本题的难度,本题还可不给单调性而增加条件比如:当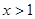 时,
时,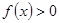 让学生自己证明函数在相应区间的单调性,进一步考查定义法证明函数单调性的方法
让学生自己证明函数在相应区间的单调性,进一步考查定义法证明函数单调性的方法

练习册系列答案
相关题目
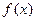 是定义在
是定义在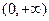 上的增函数,且对一切
上的增函数,且对一切 ,满足
,满足 .
.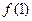 的值
的值 ,解不
,解不 等式
等式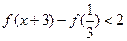 .
.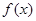 是定义在
是定义在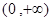 上的增函数,且对一切
上的增函数,且对一切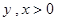 满足
满足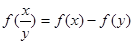
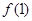
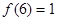 ,解不等式
,解不等式