题目内容
【题目】已知函数![]() ,且
,且![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)在函数![]() 的图象上取定两点
的图象上取定两点![]() ,
,![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,问:是否存在
,问:是否存在![]() ,使
,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的值(用
的值(用![]() 表示);若不存在,请说明理由.
表示);若不存在,请说明理由.
【答案】(Ⅰ)1(Ⅱ)存在,![]()
【解析】
(Ⅰ)讨论![]() 或
或![]() ,
,![]() 不成立,
不成立,![]() ,则
,则![]() ,利用导数与函数单调性的关系可得
,利用导数与函数单调性的关系可得![]() 的最小值,只需
的最小值,只需![]() 即可.
即可.
(Ⅱ)由题意可得![]() ,令
,令![]() ,
,![]() 在区间
在区间![]() 上单调递增,求出
上单调递增,求出![]() ,结合(Ⅰ)可得
,结合(Ⅰ)可得![]() ,
,![]() ,利用零点存在性定理即可证出.
,利用零点存在性定理即可证出.
解:(Ⅰ)若![]() ,则对一切
,则对一切![]() ,
,![]() ,这与题设矛盾;
,这与题设矛盾;
若![]() ,
,![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
故当![]() 时,
时,![]() 取最小值
取最小值![]() .
.
于是对一切![]() ,
,![]() 恒成立,当且仅当
恒成立,当且仅当![]() .①
.①
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
故当![]() 时,
时,![]() 取最大值
取最大值![]() .
.
因此,当且仅当![]() 即
即![]() 时,①式成立.
时,①式成立.
综上所述,![]() .
.
(Ⅱ)由题意知,![]() .
.
令![]() ,
,![]() 在区间
在区间![]() 上单调递增;
上单调递增;
且![]() ,
,![]() .
.
由(Ⅰ)得![]() 恒成立,
恒成立,
从而![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
由零点存在性定理得,存在唯一![]() ,使
,使![]() ,且
,且![]() .
.
综上所述,存在![]() 使
使![]() 成立,且
成立,且![]() .
.

【题目】对于很多人来说,提前消费的认识首先是源于信用卡,在那个工资不高的年代,信用卡绝对是神器,稍微大件的东西都是可以选择用信用卡来买,甚至于分期买,然后慢慢还!现在银行贷款也是很风靡的,从房贷到车贷到一般的现金贷.信用卡“忽如一夜春风来”,遍布了各大小城市的大街小巷.为了解信用卡在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下![]() 列联表(单位:人)
列联表(单位:人)
经常使用信用卡 | 偶尔或不用信用卡 | 合计 | |
40岁及以下 | 15 | 35 | 50 |
40岁以上 | 20 | 30 | 50 |
合计 | 35 | 65 | 100 |
(1)根据以上数据,能否在犯错误的概率不超过0.10的前提下认为![]() 市使用信用卡情况与年龄有关?
市使用信用卡情况与年龄有关?
(2)①现从所抽取的40岁及以下的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出4人赠送积分,求选出的4人中至少有3人偶尔或不用信用卡的概率;
②将频率视为概率,从![]() 市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为
市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为![]() ,求随机变量
,求随机变量![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
参考公式: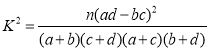 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内,武汉某制药厂在该药品的生产过程中,检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N(μ,σ2).在一天内抽取的20件产品中,如果有一件出现了主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查.
(1)下面是检验员在2月24日抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() xi=9.96,s
xi=9.96,s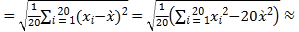 0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数
0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
(2)假设生产状态正常,记X表示某天抽取的20件产品中其主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品件数,求P(X=1)及/span>X的数学期望.
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.