题目内容
数列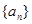 中,
中,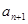 是函数
是函数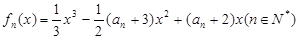 的极小值点,且
的极小值点,且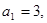
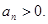
(1)求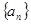 的通项公式;
的通项公式;
(2)记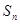 为数列
为数列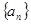 的前
的前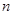 项和,试比较
项和,试比较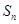 与
与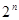 的大小关系.
的大小关系.
【答案】
(1) ;(2)
;(2)
 .
.
【解析】第一问利用函数的极值概念得到 ,从而得到递推关系式
,从而得到递推关系式 即
即
第二问中 当
当 时,
时,

 ………1分
………1分
猜想 ≥6时,
≥6时,
 ,然后运用数学归纳法证明。
,然后运用数学归纳法证明。
解:(1)由题意得: .
………1分
.
………1分
得: ,可得
,可得 ,即
,即 .………3分
.………3分
(2) ,
当
,
当 时,
时,

 ………1分
………1分
猜想 ≥6时,
≥6时,
 ………1分
………1分
下用数学归纳法证明
①当 ,
, ,成立.
,成立.
②假设当 (
( 时不等式成立,即
时不等式成立,即 ,那么………1分
,那么………1分
 ,即当
,即当 时,不等式也成立, ………2分
时,不等式也成立, ………2分
由①、②可得:对于所有的 都有
都有
 成立.………1分
成立.………1分

练习册系列答案
相关题目
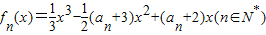 的极小值点,且a1=3,an>0.
的极小值点,且a1=3,an>0.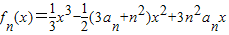 的极小值点.若数列{an}是等比数列,则a的取值范围是
的极小值点.若数列{an}是等比数列,则a的取值范围是  的极小值点.
的极小值点.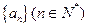 中,
中,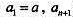 是函数
是函数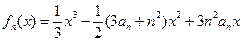 的极小值点
的极小值点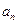 ;
; 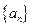 是等比数列?若存在,求a的取值范围;若不存在,请说明理由。
是等比数列?若存在,求a的取值范围;若不存在,请说明理由。