题目内容
已知函数f(x)=log2(x2-ax+3a)在[2,+∞)上是增函数,则实数a的取值范围是( )
A.(-∞,4) B.(-4,4]
C.(-∞,-4)∪[2,+∞![]() D.[-4,4)
D.[-4,4)
B
解析:
解决复合函数问题的通法是把复合函数化归为基本初等函数.
令u(x)=x2-ax+3a,其对称轴x=![]() .由题意有
.由题意有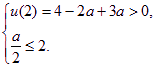 解得-4<a≤4.
解得-4<a≤4.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
题目内容
已知函数f(x)=log2(x2-ax+3a)在[2,+∞)上是增函数,则实数a的取值范围是( )
A.(-∞,4) B.(-4,4]
C.(-∞,-4)∪[2,+∞![]() D.[-4,4)
D.[-4,4)
B
解决复合函数问题的通法是把复合函数化归为基本初等函数.
令u(x)=x2-ax+3a,其对称轴x=![]() .由题意有
.由题意有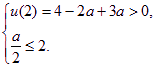 解得-4<a≤4.
解得-4<a≤4.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案