题目内容
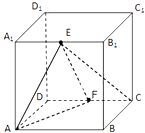 在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点.
(1)求直线EC与平面B1BCC1所成角的大小;
(2)求二面角E-AF-B的大小.
(1)解:建立坐标系如图 所示,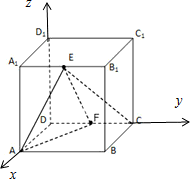
则平面B1BCC1的一个法向量为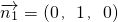
∵E(2,1,2),C(0,2,0),
∴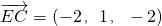 ,
,
可知直线EC的一个方向向量为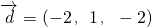 .
.
设直线EC与平面B1BCC1成角为θ,
则sinθ=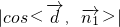 =
=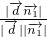 =
=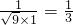 .
.
故直线EC与平面B1BCC1所成角的大小为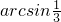 .
.
(2)由(1)可知:平面ABCD的一个法向量为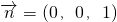 .
.
设平面AEF的一个法向量为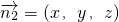 ,
,
∵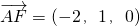 ,
, ,∴
,∴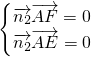 .得
.得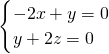 ,
,
令x=1,则y=2,z=-1 ,
,
∴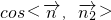 =
=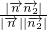 =
= =
= .
.
由图知二面角E-AF-B为锐二面角,故其大小为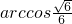 .
.
分析:(1)通过建立空间直角坐标系,利用直线的方向向量和平面的法向量的夹角即可得出线面角;
(2)利用两个平面的法向量的夹角即可得到二面角的大小.
点评:本题考查了:通过建立空间直角坐标系,利用直线的方向向量和平面的法向量的夹角得出线面角;利用两个平面的法向量的夹角得到二面角的方法.必须熟练掌握.

则平面B1BCC1的一个法向量为
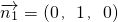
∵E(2,1,2),C(0,2,0),
∴
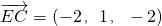 ,
,可知直线EC的一个方向向量为
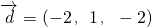 .
.设直线EC与平面B1BCC1成角为θ,
则sinθ=
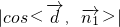 =
=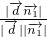 =
=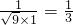 .
.故直线EC与平面B1BCC1所成角的大小为
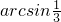 .
.(2)由(1)可知:平面ABCD的一个法向量为
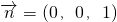 .
.设平面AEF的一个法向量为
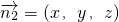 ,
,∵
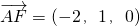 ,
, ,∴
,∴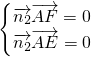 .得
.得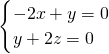 ,
,令x=1,则y=2,z=-1
 ,
,∴
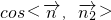 =
=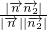 =
= =
= .
.由图知二面角E-AF-B为锐二面角,故其大小为
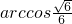 .
.分析:(1)通过建立空间直角坐标系,利用直线的方向向量和平面的法向量的夹角即可得出线面角;
(2)利用两个平面的法向量的夹角即可得到二面角的大小.
点评:本题考查了:通过建立空间直角坐标系,利用直线的方向向量和平面的法向量的夹角得出线面角;利用两个平面的法向量的夹角得到二面角的方法.必须熟练掌握.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
在棱长为2的正方体AC1中,G是AA1的中点,则BD到平面GB1D1的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( ) (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).
(2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).