题目内容
若三点O、A、B不共线，则“存在唯一一对实数λ1、λ2，使
=λ1
+λ2
”是“P点在直线AB上”的（ ）
| OP |
| OA |
| OB |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
分析：根据向量法判断三点共线的充要条件，我们可以写出“P点在直线AB上”的充要条件，分析与“存在唯一一对实数λ1、λ2，使
=λ1
+λ2
”的关系后，即可得到答案．
| OP |
| OA |
| OB |
解答：解：根据向量法判断三点共线的充要条件，
当“P点在直线AB上”?“存在唯一一对实数λ1、λ2，使
=λ1
+λ2
，且λ1+λ2=1”
故“存在唯一一对实数λ1、λ2，使
=λ1
+λ2
”是“P点在直线AB上”必要不充分条件
故选B
当“P点在直线AB上”?“存在唯一一对实数λ1、λ2，使
| OP |
| OA |
| OB |
故“存在唯一一对实数λ1、λ2，使
| OP |
| OA |
| OB |
故选B
点评：本题考查的知识点是必要条件，充分条件与充要条件的判断，平面向量的基本定理及其意义，其中熟练掌握向量法判断三点共线的充要条件，是解答本题的关键．
练习册系列答案
特高级教师点拨系列答案
相关题目
、
，使
”是“P点在直线AB上”的
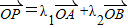”是“P点在直线AB上”的（ ）
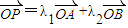”是“P点在直线AB上”的（ ）