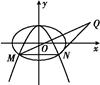
题目内容
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 , 焦距为2,过
, 焦距为2,过 作垂直于椭圆长轴的弦长
作垂直于椭圆长轴的弦长 为3
为3
(1)求椭圆的方程;
(2)若过点 的动直线
的动直线 交椭圆于A、B两点,判断是否存在直线
交椭圆于A、B两点,判断是否存在直线 使得
使得 为钝角,若存在,求出直线
为钝角,若存在,求出直线 的斜率
的斜率 的取值范围
的取值范围
(1)椭圆方程为 ;(2)存在定点
;(2)存在定点 ,使以AB为直径的圆恒过点
,使以AB为直径的圆恒过点
解析试题分析:(1) 过
过 作垂直于椭圆长轴的弦长为
作垂直于椭圆长轴的弦长为 ,由此可得
,由此可得 ,解得
,解得 ,从而可得椭圆的方程 (2)首先考虑直线
,从而可得椭圆的方程 (2)首先考虑直线 的斜率不存在的情况 当过
的斜率不存在的情况 当过 直线
直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为 ,设
,设 , 由
, 由 得:
得: 当
当 为钝角时,
为钝角时,
 ,利用韦达定理将不等式化为含
,利用韦达定理将不等式化为含 的不等式,解此不等式即可得
的不等式,解此不等式即可得 的取值范围
的取值范围
试题解析:(1) 依题意
依题意 (2分)
(2分)
解得 ,∴椭圆的方程为:
,∴椭圆的方程为: (4分)
(4分)
(2)(i)当过 直线
直线 的斜率不存在时,点
的斜率不存在时,点 ,
,
则 ,显然
,显然 不为钝角 (5分)
不为钝角 (5分)
(ii)当过 直线
直线 的斜率存在时,设斜率为
的斜率存在时,设斜率为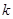 ,则直线
,则直线 的方程为
的方程为 ,
,
设 , 由
, 由 得:
得:
 恒成立
恒成立  (8分)
(8分)
 (11分)
(11分)
当 为钝角时,
为钝角时, <0,
<0,
综上所述,满足条件的直线斜率k满足 且
且 (13分)
(13分)
考点:直线与圆锥曲线

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为
的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为 ,
,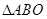 的面积为
的面积为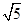 .
.
 交椭圆于P、Q两点,
交椭圆于P、Q两点, ,求直线
,求直线
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
 ,且其三个顶点均在抛物线E:x2=2py(p>0)上.
,且其三个顶点均在抛物线E:x2=2py(p>0)上.
 )和
)和 ,并且经过点
,并且经过点 ,抛物线的顶点E在坐标原点,焦点恰好是椭圆C的右顶点F.
,抛物线的顶点E在坐标原点,焦点恰好是椭圆C的右顶点F. 的最小值.
的最小值. +
+ =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.