题目内容
9.已知二次函数y=x2+ax+1与x轴的正半轴有两个不同的交点,则实数a的取值范围是( )| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2) | C. | (2,+∞) | D. | (-∞,0) |
分析 由题意可得x2+ax+1=0有两个不相等的正根,即有△>0,x1+x2>0,x1x2>0,运用韦达定理,解不等式即可得到所求a的范围.
解答 解:由题意可得x2+ax+1=0有两个不相等的正根,
即有△>0,x1+x2>0,x1x2>0,
即为a2-4>0,-a>0,1>0,
解得a<-2.
故选B.
点评 本题考查二次函数的性质和运用,考查函数方程的转化思想的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.设等差数列{an}的公差为d,则a1d>0是数列{${3}^{{a}_{1}{a}_{n}}$}为递增数列的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
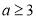 ,函数
,函数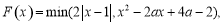 其中
其中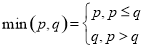 .
.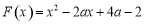 成立的
成立的 的取值范围;
的取值范围;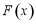 的最小值
的最小值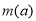 ;
;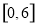 上的最大值
上的最大值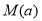 .
. 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过 的直线交椭圆于A、B两点若
的直线交椭圆于A、B两点若 ,则
,则 =_____.
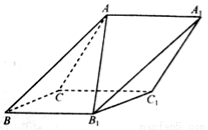
=_____.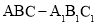 中,侧面
中,侧面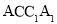 与侧面
与侧面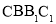 都是菱形,
都是菱形,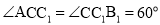 ,
,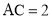 .
.
 求证:
求证: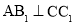 ;
; 若
若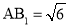 ,求二面角
,求二面角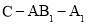 的余弦值.
的余弦值. 和
和 的前
的前 项和分别为
项和分别为 和
和 ,已知
,已知 ,
,
 ,其中
,其中 。
。 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 。当
。当 .
.