题目内容
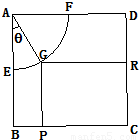
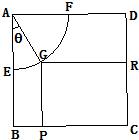 现将边长为2米的正方形铁片ABCD裁剪成一个半径为1米的扇形
现将边长为2米的正方形铁片ABCD裁剪成一个半径为1米的扇形 |
| AEF |
 |
| EF |
 |
| EF |
分析:先利用线段之间的关系求出矩形CRGP的面积S关于θ的函数关系式,再借助于θ的取值范围以及二次函数在闭区间上求最值的方法即可求出矩形面积最大值.
解答:解:延长RG交AB于点M,则GP=AB-AM=2-cosθ,PC=BC-MG=2-sinθ,
于是,S=GP•PC=4-2(sinθ+cosθ)+sinθ•cosθ
令t=sinθ+cosθ=
sin(θ+45°),则sinθcosθ=
,
所以S=4-2t+
=
(t-2)2+
.
∵00≤θ≤900
∴1≤t≤
∴当t=1,即θ=0°或90°时,S有最大值2,
此时点G在
的中点,矩形面积最大值为2.
于是,S=GP•PC=4-2(sinθ+cosθ)+sinθ•cosθ
令t=sinθ+cosθ=
| 2 |
| t2-1 |
| 2 |
所以S=4-2t+
| t2-1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵00≤θ≤900
∴1≤t≤
| 2 |
∴当t=1,即θ=0°或90°时,S有最大值2,
此时点G在
 |
| EF |
点评:本题主要考查三角函数知识的应用问题.解决本题的关键在于求出矩形CRGP的面积S关于θ的函数关系式.

练习册系列答案
相关题目
 裁剪成一个半径为1米的扇形
裁剪成一个半径为1米的扇形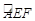 和一个矩形
和一个矩形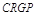 ,如图所示,点
,如图所示,点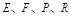 分别在
分别在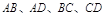 上,点
上,点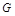 在
在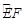 上.设矩形
上.设矩形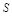 ,
,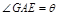 ,试将
,试将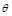 的函数,并指出点
的函数,并指出点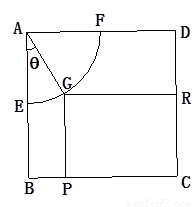
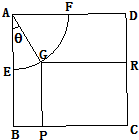 现将边长为2米的正方形铁片ABCD裁剪成一个半径为1米的扇形
现将边长为2米的正方形铁片ABCD裁剪成一个半径为1米的扇形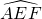 和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在
和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在 上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在
上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在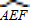 和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在
和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在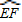 上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在
上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在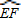 的何处时,矩形面积最大,并求之.
的何处时,矩形面积最大,并求之.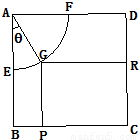
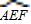 和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在
和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在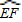 上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在
上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在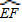 的何处时,矩形面积最大,并求之.
的何处时,矩形面积最大,并求之.