题目内容
设![]() ,其中a为正实数
,其中a为正实数
(Ⅰ)当a=![]() 时,求f(x)的极值点;
时,求f(x)的极值点;
(Ⅱ)若f(x)为R上的单调函数,求a的取值范围.
考点:
利用导数研究函数的极值;利用导数研究函数的单调性;一元二次不等式的解法.
专题:
计算题.
分析:
(Ⅰ)首先对f(x)求导,将a=![]() 代入,令f′(x)=0,解出后判断根的两侧导函数的符号即可.
代入,令f′(x)=0,解出后判断根的两侧导函数的符号即可.
(Ⅱ)因为a>0,所以f(x)为R上为增函数,f′(x)≥0在R上恒成立,转化为二次函数恒成立问题,只要△≤0即可.
解答:
解:对f(x)求导得
f′(x)=![]() ×ex
×ex
(Ⅰ)当a=![]() 时,若f′(x)=0,则4x2﹣8x+3=0,解得
时,若f′(x)=0,则4x2﹣8x+3=0,解得
![]()
结合①,可知
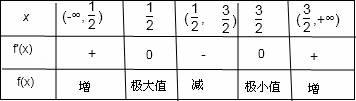
所以,![]() 是极小值点,
是极小值点,![]() 是极大值点.
是极大值点.
(Ⅱ)若f(x)为R上的单调函数,则f′(x)在R上不变号,
结合①与条件a>0知ax2﹣2ax+1≥0在R上恒成立,
因此△=4a2﹣4a=4a(a﹣1)≤0,由此并结合a>0,知0<a≤1.
点评:
本题考查求函数的极值问题、已知函数的单调性求参数范围问题,转化为不等式恒成立问题求解.

练习册系列答案
相关题目
 ,其中a为正实数。
,其中a为正实数。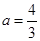 时,求
时,求 的极值点;
的极值点; ,其中a为正实数,
,其中a为正实数, 的极值点;
的极值点; 为R上的单调函数,求a的取值范围。
为R上的单调函数,求a的取值范围。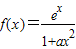 ,其中a为正实数
,其中a为正实数 时,求f(x)的极值点;
时,求f(x)的极值点; ,其中a为正实数
,其中a为正实数 时,求f(x)的极值点;
时,求f(x)的极值点; ,其中a为正实数
,其中a为正实数 时,求f(x)的极值点;
时,求f(x)的极值点;