题目内容
已知抛物线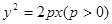 .过动点M(
.过动点M(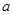 ,0)且斜率为1的直线
,0)且斜率为1的直线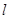 与该抛物线交于不同的两点A、B,
与该抛物线交于不同的两点A、B,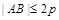 .
.
(Ⅰ)求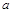 的取值范围;
的取值范围;
(Ⅱ)若线段AB的垂直平分线交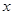 轴于点N,求
轴于点N,求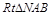 面积的最大值.(14分)
面积的最大值.(14分)
【答案】
(1)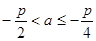 ;(2)
;(2)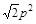 .
.
【解析】
试题分析:(Ⅰ)直线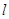 的方程为
的方程为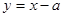 ,将
,将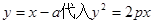 ,
,
得  . 设直线
. 设直线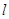 与抛物线两个不同交点的坐标为
与抛物线两个不同交点的坐标为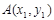 、
、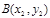 ,
,
则 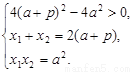 又
又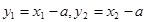 ,
,
∴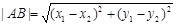
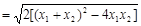
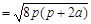 . ∵
. ∵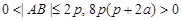 , ∴
, ∴ 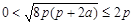 . 解得
. 解得 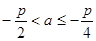 .
. 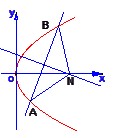
(Ⅱ)设AB的垂直平分线交AB于点Q,令坐标为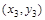 ,则由中点坐标公式,得
,则由中点坐标公式,得
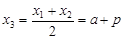 ,
, 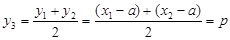 .
.
∴ 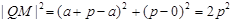 . 又
. 又 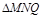 为等腰直角三角形,
为等腰直角三角形,
∴ 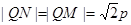 , ∴
, ∴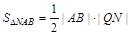
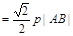
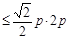
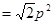
即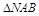 面积最大值为
面积最大值为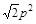
考点:本题主要考查抛物线的标准方程、几何性质及直线与抛物线的位置关系,考查了中点坐标公式。
点评:这是一道综合性较强的题目,在重点考查直线与抛物线位置关系的同时,考查了中点坐标公式的应用,对考生分析问题解决问题的能力及运算能力都有较好的考查功能。

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
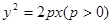 .过动点M(
.过动点M(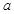 ,0)且斜率为1的直线
,0)且斜率为1的直线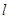 与该抛物线交于不同的两点A、B,
与该抛物线交于不同的两点A、B,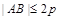 .
.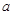 的取值范围。
的取值范围。 .过动点M(
.过动点M( ,0)且斜率为1的直线
,0)且斜率为1的直线 与该抛物线交于不同的两点A、B,
与该抛物线交于不同的两点A、B, .
. 的取值范围。
的取值范围。