题目内容
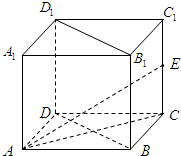 已知:正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点.
已知:正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点.(Ⅰ)求证:AC∥平面B1DE;
(Ⅱ)求三棱锥A-BDE的体积.
分析:(1)作BB1的中点F,连接AF、CF、EF,由三角形中位线定理,我们易证明AF∥ED,CF∥B1E.结合面面垂直的判定定理可得平面ACF∥面B1DE,再由面面平行的性质得到AC∥平面B1DE;
(Ⅱ)由(1)的结论,由三棱锥的几何特征,我们可得三棱锥A-BDE的体积VA-BDE=VE-ABD=
S△ABD•CE,计算出底面面积及棱锥的高,代入体积公式即可得到答案.
(Ⅱ)由(1)的结论,由三棱锥的几何特征,我们可得三棱锥A-BDE的体积VA-BDE=VE-ABD=
| 1 |
| 3 |
解答: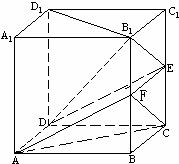 解:(Ⅰ)证明:作BB1的中点F,连接AF、CF、EF.
解:(Ⅰ)证明:作BB1的中点F,连接AF、CF、EF.
∵E、F是CC1、BB1的中点,∴CE∥B1F,且CE=B1F,(1分)
∴四边形B1FCE是平行四边形,∴CF∥B1E.(2分)
∵E,F是CC1、BB1的中点,∴EF
BC,(3分)
又BC
AD,∴EF
AD.
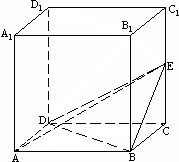 ∴四边形ADEF是平行四边形,∴AF∥ED,(5分)
∴四边形ADEF是平行四边形,∴AF∥ED,(5分)
∵AF∩CF=F,B1E∩ED=E,
∴平面ACF∥面B1DE.(6分)
又AC?平面ACF,∴AC∥面B1DE.(7分)
(Ⅱ)S△ABD=
AB•AD=2. (8分)VA-BDE=VE-ABD=
S△ABD•CE=
S△ABD•CE=
.(12分)
 解:(Ⅰ)证明:作BB1的中点F,连接AF、CF、EF.
解:(Ⅰ)证明:作BB1的中点F,连接AF、CF、EF.∵E、F是CC1、BB1的中点,∴CE∥B1F,且CE=B1F,(1分)
∴四边形B1FCE是平行四边形,∴CF∥B1E.(2分)
∵E,F是CC1、BB1的中点,∴EF
| ||
. |
又BC
| ||
. |
| ||
. |
 ∴四边形ADEF是平行四边形,∴AF∥ED,(5分)
∴四边形ADEF是平行四边形,∴AF∥ED,(5分)∵AF∩CF=F,B1E∩ED=E,
∴平面ACF∥面B1DE.(6分)
又AC?平面ACF,∴AC∥面B1DE.(7分)
(Ⅱ)S△ABD=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,证明线面平行有两种办法,一是利用线面平行的判定定理,本题较难实现;二是先证明面面平行,再根据面面平行的性质,得到线面平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
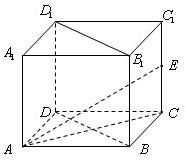 已知:正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点.
已知:正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点. 已知单位正方体ABCD-A1B1C1D1,E分别是棱C1D1的中点,试求:
已知单位正方体ABCD-A1B1C1D1,E分别是棱C1D1的中点,试求: 已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=
已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG= (2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1.
(2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1.