题目内容
直线l：y=k（x-2）+4与曲线C：y=1+
有两个交点，则k的取值范围
| 4-x2 |
（
，
]
| 5 |
| 12 |
| 3 |
| 4 |
（
，
]
．| 5 |
| 12 |
| 3 |
| 4 |
分析：根据直线方程的点斜式和圆的方程，可得直线l经过点A（2，4），曲线C表示以（0，1）圆心半径为2的圆的上半圆．由此作出图形，求出半圆切线的斜率和直线与半圆相交时斜率的最小值，结合图形加以观察即可得到本题答案．
解答：解：∵直线l：y=k（x-2）+4经过定点A（2，4）
曲线C：y=1+
化简得x2+（y-1）2=4，
表示以（0，1）圆心半径为2的圆的上半圆
∴直线l与曲线C有两个交点，即直线与半圆相交
求得当直线与半圆相切时，斜率k=
当直线l为经过点B（-2，1）时，是斜率k的最大值，此时k=
动直线l位于切线与AB之间（包括AB）时，直线l与曲线C有两个交点，
∴k的取值范围为（
，
]
故答案为：（
，
]
曲线C：y=1+
| 4-x2 |
表示以（0，1）圆心半径为2的圆的上半圆
∴直线l与曲线C有两个交点，即直线与半圆相交
求得当直线与半圆相切时，斜率k=
| 5 |
| 12 |
当直线l为经过点B（-2，1）时，是斜率k的最大值，此时k=
| 3 |
| 4 |
动直线l位于切线与AB之间（包括AB）时，直线l与曲线C有两个交点，
∴k的取值范围为（
| 5 |
| 12 |
| 3 |
| 4 |
故答案为：（
| 5 |
| 12 |
| 3 |
| 4 |
点评：本题以两条曲线有两个交点为例，求斜率k的范围，着重考查了直线的方程、圆的方程和直线与圆的位置关系等知识，属于中档题．
练习册系列答案
相关题目
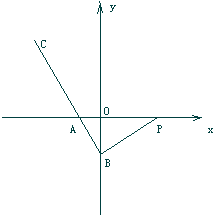如图，已知直角三角形PAB的直角顶点为B，点P的坐标为（3，0），点B在y轴上，点A在x轴的负半轴上，在BA的延长线上取一点C，使