Question

【题目】三棱锥的一条棱长为，其余棱长均为2，当三棱锥的体积最大时, 它的外接球的表面积为（ ）

A. B. C. D.

Answer 1

【答案】B

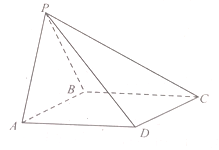
【解析】由题意画出三棱锥的图形，

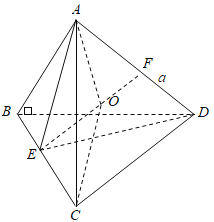
其中AB=BC=CD=BD=AC=2，AD=m；

取BC，AD的中点分别为E，F，

可知AE⊥BC，DE⊥BC，

且AE∩DE=E，

∴BC⊥平面AED，

∴平面ABC⊥平面BCD时，三棱锥A﹣BCD的体积最大，

此时AD=m=AE=×=；

设三棱锥外接球的球心为O，半径为R，由球体的对称性知，

球心O在线段EF上，

∴OA=OC=R，又EF===，

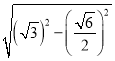设OF=x，OE=﹣x，

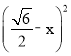∴R2=+x2=+1，

解得x=；

∴球的半径R满足R2=，

∴三棱锥外接球的表面积为4πR2=4π×=．

故选：B．