题目内容
设函数f（x）=e2x-2x，则
=
| lim |
| x→0 |
| f′(x) |
| ex-1 |
4
4
．分析：由f（x）=e2x-2x，知f′（x）=2e2x-2=2（ex-1）（ex+1），
=
=
2(ex+1)，由此能求出其结果．
| lim |
| x→0 |
| f′(x) |
| ex-1 |
| lim |
| x→0 |
| 2(ex-1)(ex+1) |
| ex-1 |
| lim |
| x→0 |
解答：解：∵f（x）=e2x-2x，
∴f′（x）=2e2x-2=2（ex-1）（ex+1），
∴
=
=
2(ex+1)
=4．
故答案为：4．
∴f′（x）=2e2x-2=2（ex-1）（ex+1），
∴
| lim |
| x→0 |
| f′(x) |
| ex-1 |
=
| lim |
| x→0 |
| 2(ex-1)(ex+1) |
| ex-1 |
=
| lim |
| x→0 |
=4．
故答案为：4．
点评：本题考查极限的运算的应用，解题时要认真审题，仔细解答，注意导数的灵活运用．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
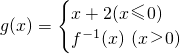，则g[g（-1）]=________．
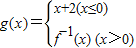，则g[g（-1）]= ．
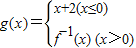，则g[g（-1）]= ．