ЬтФПФкШн
ЯТСаУќЬтжаЃЌецУќЬтЪЧ
ЂйШєfЁфЃЈx0ЃЉ=0ЃЌдђКЏЪ§fЃЈxЃЉдкx=x0ДІШЁМЋжЕЃЎ
ЂкКЏЪ§fЃЈxЃЉ=lnx+x-2дкЧјМфЃЈ1ЃЌeЃЉЩЯДцдкСуЕуЃЎ
ЂлЁАa=1ЁБЪЧКЏЪ§f(x)=
дкЖЈвхгђЩЯЪЧЦцКЏЪ§ЕФГфЗжВЛБивЊЬѕМўЃЎ
ЂмНЋКЏЪ§y=2cos2x-1ЕФЭМЯѓЯђгвЦНвЦ
ИіЕЅЮЛПЩЕУЕНy=sin2xЕФЭМЯѓЃЎ
ЂнЕу(
ЃЌ
)ЪЧКЏЪ§f(x)=cos
x(
sin
x+cos
x)ЭМЯѓЕФвЛИіЖдГЦжааФЃЎ
ЂкЂл
ЂкЂл
ЃЎЂйШєfЁфЃЈx0ЃЉ=0ЃЌдђКЏЪ§fЃЈxЃЉдкx=x0ДІШЁМЋжЕЃЎ
ЂкКЏЪ§fЃЈxЃЉ=lnx+x-2дкЧјМфЃЈ1ЃЌeЃЉЩЯДцдкСуЕуЃЎ
ЂлЁАa=1ЁБЪЧКЏЪ§f(x)=
| a-ex |
| 1+aex |
ЂмНЋКЏЪ§y=2cos2x-1ЕФЭМЯѓЯђгвЦНвЦ
| 3Іа |
| 4 |
ЂнЕу(
| Іа |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
ЗжЮіЃКСюfЃЈxЃЉ=x3ЃЌПЩХаЖЯЂйДэЮѓЃЛИљОнКЏЪ§СуЕуДцдкЖЈРэЃЌПЩХаЖЯЂкДэЮѓЃЛИљОнЦцКЏЪ§ЕФЖЈвхЧѓГіaжЕЃЌРћгУГфвЊЬѕМўЕФЖЈвхЃЌПЩХаЖЯЂлЕФецМйЃЌИљОнКЏЪ§ЭМЯѓЦНвЦБфЛЛЗЈдђЃЌЧѓГіЦНвЦКѓКЏЪ§ЕФНтЮіЪНЃЌЖдееКѓПЩХаЖЯЂмЕФецМйЃЌИљОне§ЯваЭКЏЪ§ЕФЖдГЦадЃЌНЋЕуЕФКсзјБъДњШыПЩХаЖЯЂнЕФецМйЃЎ
НтД№ЃКНтЃКСюfЃЈxЃЉ=x3ЃЌдђfЁфЃЈx0ЃЉ=3x2ЃЌЕБx=0ЪБЃЌfЁфЃЈxЃЉ=0ЃЌДЫЪБКЏЪ§fЃЈxЃЉВЛЪЧМЋжЕЃЌЙЪЂйДэЮѓЃЛ
КЏЪ§fЃЈxЃЉ=lnx+x-2дкЧјМфЃЈ1ЃЌeЃЉЩЯЪЧСЌајЕФЃЌЧвfЃЈ1ЃЉ=-1ЃМ0ЃЌfЃЈeЃЉ=e-1ЃО0ЃЌИљОнКЏЪ§СуЕуДцдкЖЈРэЃЌПЩЕУКЏЪ§дкЧјМфЃЈ1ЃЌeЃЉЩЯДцдкСуЕуЃЌЙЪЂке§ШЗЃЛ
КЏЪ§f(x)=
дкЖЈвхгђЩЯЪЧЦцКЏЪ§ЃЌдђf(-x)=
=
=-f(x)=-
ЃЌМДНтЕУa=ЁР1ЃЌЙЪЂлЁАa=1ЁБЪЧКЏЪ§f(x)=
дкЖЈвхгђЩЯЪЧЦцКЏЪ§ЕФГфЗжВЛБивЊЬѕМўе§ШЗЃЛ
НЋКЏЪ§y=2cos2x-1=cos2xЕФЭМЯѓЯђгвЦНвЦ
ИіЕЅЮЛПЩЕУЕНy=cos[2ЃЈx-
ЃЉ]=cosЃЈ2x-
ЃЉ=-sin2xЕФЭМЯѓЃЌЙЪЂмДэЮѓЃЎ
ЕБx=
ЪБЃЌКЏЪ§f(x)=cos
x(
sin
x+cos
x)=sin(x+
)+
=
ЃЌДЫЪБКЏЪ§ШЁзюДѓжЕЃЌЙЪЂнДэЮѓ
ЙЪД№АИЮЊЂкЂл
КЏЪ§fЃЈxЃЉ=lnx+x-2дкЧјМфЃЈ1ЃЌeЃЉЩЯЪЧСЌајЕФЃЌЧвfЃЈ1ЃЉ=-1ЃМ0ЃЌfЃЈeЃЉ=e-1ЃО0ЃЌИљОнКЏЪ§СуЕуДцдкЖЈРэЃЌПЩЕУКЏЪ§дкЧјМфЃЈ1ЃЌeЃЉЩЯДцдкСуЕуЃЌЙЪЂке§ШЗЃЛ
КЏЪ§f(x)=
| a-ex |
| 1+aex |
| a-e-x |
| 1+ae-x |
| aex-1 |
| ex+a |
| a-ex |
| 1+aex |
| a-ex |
| 1+aex |
НЋКЏЪ§y=2cos2x-1=cos2xЕФЭМЯѓЯђгвЦНвЦ
| 3Іа |
| 4 |
| 3Іа |
| 4 |
| 3Іа |
| 2 |
ЕБx=
| Іа |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| Іа |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
ЙЪД№АИЮЊЂкЂл
ЕуЦРЃКБОЬтЪЧУќЬтЕФецМйХаЖЯЮЊдиЬхПМВщСЫКЏЪ§ШЁМЋжЕЕФЬѕМўЃЌКЏЪ§ЕФСуЕуЃЌЦцКЏЪ§ЕФЖЈвхЃЌКЏЪ§ЭМЯѓЕФЦНвЦЃЌКЏЪ§ЕФЖдГЦадЃЌЪЧКЏЪ§гыТпМЕФзлКЯгІгУЃЎ

СЗЯАВсЯЕСаД№АИ
 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
ЯрЙиЬтФП
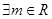 ЃЌЪЙКЏЪ§
ЃЌЪЙКЏЪ§ ЪЧХМКЏЪ§
ЪЧХМКЏЪ§ ЃЌЪЙКЏЪ§
ЃЌЪЙКЏЪ§ Ём0
Ём0 =-1
=-1