题目内容
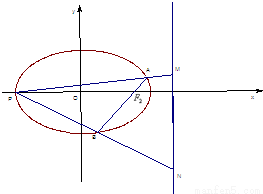
如图，A为椭圆
上的一个动点，弦AB、AC分别过焦点F1、F2．当AC垂直于x轴 时，恰好|AF1|:|AF2=3:1（I）求该椭圆的离心率；（II）设
，
，试判断l1+l2是否为定值？若是，则求出该定值；若不是，请说明理由．
（I）
（II）l1+l2是定值6
解析:
：（I）当
C垂直于x轴时，
，由
，
得
，
在Rt△
中，
解得 
=．
（II）由=
，则
，
．
焦点坐标为
，则椭圆方程为
，
化简有
．设
，
，
①若直线AC的斜率存在，则直线AC方程为
代入椭圆方程有
．
由韦达定理得：
，∴
所以
，同理可得
故l1+l2=
．②若直线
轴，
，
，
∴l1+l2＝6． 综上所述：l1+l2是定值6．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
如图，F1，F2是椭圆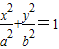
（a＞b＞0）上的焦点，P为椭圆上的点，PF1⊥OX轴，且OP和椭圆的一条长轴顶点A和短轴顶点B的连线AB平行．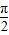
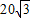，求椭圆方程．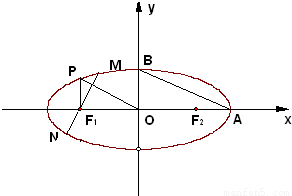
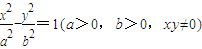上的动点，F1、F2是双曲线的焦点，M是∠F1PF2的平分线上的一点，且
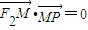．有一同学用以下方法研究|OM|：延长F2M交PF1于点N，可知△PNF2为等腰三角形，且M为F2N的中点，得
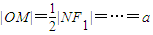．类似地：P是椭圆
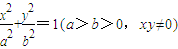上的动点，F1、F2是椭圆的焦点，M是∠F1PF2的平分线上的一点，且
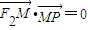．则|OM|的取值范围是（ ）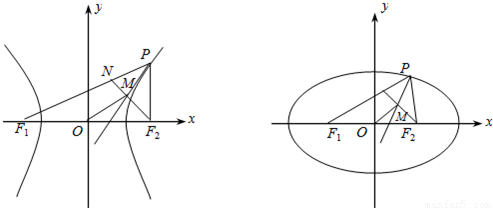
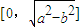
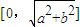
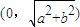
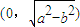
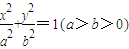上的一个动点，F1，F2分别为椭圆的左、右焦点，弦AB过点F2，当AB⊥x轴时，恰好有|AF1|=3|AF2|．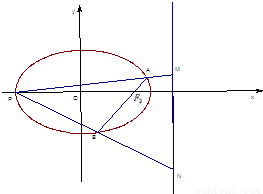
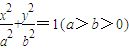上的一个动点，F1，F2分别为椭圆的左、右焦点，弦AB过点F2，当AB⊥x轴时，恰好有|AF1|=3|AF2|．