题目内容
已知△ABC的内角A、B、C的对边分别为a、b、c, sin Ccos C-cos2C=
sin Ccos C-cos2C= ,且c=3.
,且c=3.
(1)求角C;
(2)若向量m=(1,sin A)与n=(2,sin B)共线,求a、b的值.
 sin Ccos C-cos2C=
sin Ccos C-cos2C= ,且c=3.
,且c=3.(1)求角C;
(2)若向量m=(1,sin A)与n=(2,sin B)共线,求a、b的值.
(1) (2)
(2)
 (2)
(2)
(1)∵ sin Ccos C-cos2C=
sin Ccos C-cos2C= ,
,
∴ sin 2C-
sin 2C- cos 2C=1,即sin2C-
cos 2C=1,即sin2C- =1,
=1,
∵0<C<π,∴2C- =
= ,解得C=
,解得C= .
.
(2)∵m与n共线,∴sin B-2sin A=0,
由正弦定理 =
= ,得b=2a,①
,得b=2a,①
∵c=3,由余弦定理,得9=a2+b2-2abcos ,②
,②
联立方程①②,得
 sin Ccos C-cos2C=
sin Ccos C-cos2C= ,
,∴
 sin 2C-
sin 2C- cos 2C=1,即sin2C-
cos 2C=1,即sin2C- =1,
=1,∵0<C<π,∴2C-
 =
= ,解得C=
,解得C= .
.(2)∵m与n共线,∴sin B-2sin A=0,
由正弦定理
 =
= ,得b=2a,①
,得b=2a,①∵c=3,由余弦定理,得9=a2+b2-2abcos
 ,②
,②联立方程①②,得


练习册系列答案
相关题目

 .
. 的值;
的值; 时,求
时,求 ,
, .
. 的值;(2)若
的值;(2)若 ,
, ,求
,求 .
. ,且α∈
,且α∈ ,则tan(2π-α)的值为________.
,则tan(2π-α)的值为________.
 ;
; 是第三象限角,且
是第三象限角,且 ,求
,求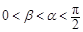 ,且
,且 ,则
,则 的值为 .
的值为 . 是第四象限角,
是第四象限角, ,则
,则 ( )
( )



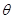 是△ABC的一个内角,且sin θcos θ=-
是△ABC的一个内角,且sin θcos θ=-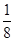 ,则sin θ-cos θ的值为( )
,则sin θ-cos θ的值为( )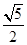
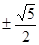
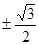
 ,则
,则 ( )
( )

