Question

已知f（x）=|x²-4x+3|，且g（x）=f（x）-mx有4个不同的零点，则m的取值范围是________．

Answer 1

分析：作出函数f（x）=|x²-4x+3|的图象，再分类讨论，即可得到结论．
解答：f（x）=|（x-2）²-1|，函数图象如图，

设y=mx，则
当m=0，有y=0与f（x）有两个交点
当y与f（x）在（1，3）上相切，与f（x）有三个交点
令F（x）=f（x）-mx=-x²+（4-m）x-3，则由△=（4-m）²-12=0，解得m₁=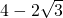，m₂=
若m=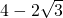代入F（x），解得x=∈（1，3）
若m=代入F（x），解得x=-∉（1，3）（舍去）
故m=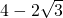时，y与f（x）有三个交点；当0＜m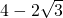＜时，y与f（x）有四个交点；当m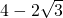＞时 y与f（x）有两个交点；当m＜0时 y与f（x）一定不会有四个交点
综上所述，m的取值范围是
故答案为：．
点评：本题考查函数的零点，考查数形结合的数学思想，考查学生分析解决问题的能力，属于中档题．