Question

如图所示，在直三棱柱ABC－A₁B₁C₁中，∠ACB=90°，CB=1，CA=，AA₁=，M是侧棱CC₁上一点，AM⊥BA₁．

(1)求证AM⊥平面A₁BC；

(2)求二面角B―AM―C的大小．

Answer 1

解：(1)在三棱柱ABC―A₁B₁C₁中，易知平面ACC₁A₁⊥平面ABC于AC，因为∠ACB=90°，∴BC⊥AC又AM平面ACC_lA₁，所以BC⊥AM，因为AM⊥BA₁，且BC∩BA₁=B，

所以AM⊥平面A₁BC

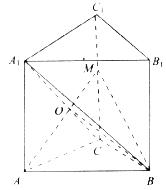
(2)设AM与A₁C的交点为O，连接BO，如图所示，由(1)知AM⊥OB，且AM⊥OC，所以∠BOC为二面角B―AM―C的平面角，

在Rt△ACM和Rt△A₁AC中，∠MAC+∠ACO=90°，∠AA₁C+∠ACO=90°，

∴∠AA₁C=∠MAC，所以Rt△ACM∽Rt△A₁AC，所以AC² =MC?AA₁ ，

所以MC=，所以在Rt△ACM中，AM=，

因为AC?MC=AM?CO，所以CO=1，所以在Rt△BCO中，tan∠BOC=1，

所以∠BOC=45°，故所求二面角的大小为45°(也可以建立空间直角坐标系来求解)．