题目内容
设函数f(x)=x2-2x+3,g(x)=x2-x。
(1)解不等式|f(x)-g(x)|≥2011;
(2)若|f(x)-a|<2恒成立的充分条件是1≤x≤2,求实数a的取值范围。
(1)解不等式|f(x)-g(x)|≥2011;
(2)若|f(x)-a|<2恒成立的充分条件是1≤x≤2,求实数a的取值范围。
解:(1)由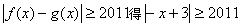
即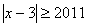
所以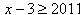 或
或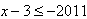
解得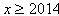 或
或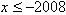 ;
;
(2)依题意知:当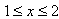 时,
时,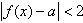 恒成立
恒成立
所以当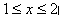 时,
时,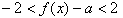 恒成立
恒成立
即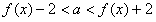 恒成立
恒成立
由于当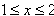 时,
时,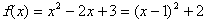 的最大值为3,最小值为2,
的最大值为3,最小值为2,
因此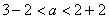
即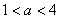
所以实数a的取值范围(1,4)。
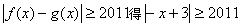
即
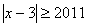
所以
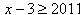 或
或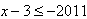
解得
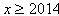 或
或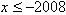 ;
;(2)依题意知:当
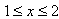 时,
时,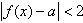 恒成立
恒成立所以当
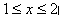 时,
时,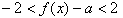 恒成立
恒成立即
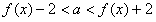 恒成立
恒成立由于当
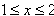 时,
时,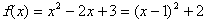 的最大值为3,最小值为2,
的最大值为3,最小值为2,因此
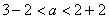
即
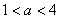
所以实数a的取值范围(1,4)。

练习册系列答案
相关题目