题目内容
已知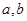 是正实数,设函数
是正实数,设函数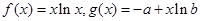 。
。
(Ⅰ)设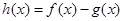 ,求
,求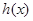 的单调区间;
的单调区间;
(Ⅱ)若存在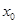 ,使
,使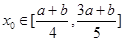 且
且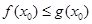 成立,求
成立,求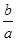 的取值范围。
的取值范围。
【答案】
(Ⅰ)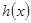 在
在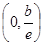 上单调递减,在
上单调递减,在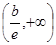 上单调递增;(Ⅱ)
上单调递增;(Ⅱ)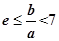 .
.
【解析】
试题分析:(Ⅰ)首先求得函数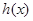 的解析式,然后求导,根据导数的正负求函数的单调区间;(Ⅱ)本小题首先考虑把
的解析式,然后求导,根据导数的正负求函数的单调区间;(Ⅱ)本小题首先考虑把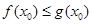 化为使
化为使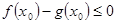 ,即存在
,即存在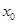 ,使
,使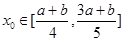 时
时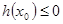 ,所以只需
,所以只需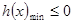 即可,于是利用导数分析单调性然后求在区间上的最小值.
即可,于是利用导数分析单调性然后求在区间上的最小值.
试题解析:(Ⅰ)由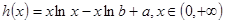 可得
可得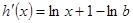
由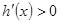 得
得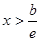
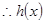 在
在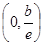 上单调递减,在
上单调递减,在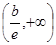 上单调递增
上单调递增
(Ⅱ)由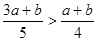 得
得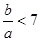
①当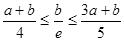 ,即
,即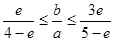 时
时
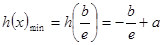
由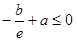 得
得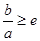
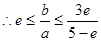
②当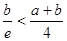 时,
时,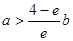
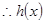 在
在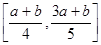 上单调递增
上单调递增
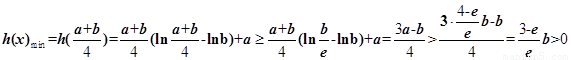
所以不成立 12分
③当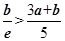 ,即
,即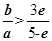 时,
时,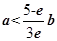
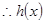 在
在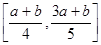 上单调递减
上单调递减
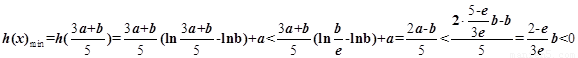
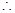 当
当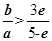 时恒成立
14分
时恒成立
14分
综上所述,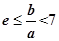 15分
15分
考点:1.导数判断单调性;2.函数的最值;3.分类讨论.

练习册系列答案
相关题目
已知a,b是正实数,设函数f(x)=xlnx,g(x)=-a+xlnb.
(Ⅰ)设h(x)=f(x)-g(x),求h(x)的单调区间;
(Ⅱ)若存在x,使x∈[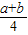 ,
,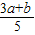 ]且f(x)≤g(x)成立,求
]且f(x)≤g(x)成立,求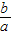 的取值范围.
的取值范围.
(Ⅰ)设h(x)=f(x)-g(x),求h(x)的单调区间;
(Ⅱ)若存在x,使x∈[
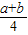 ,
,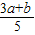 ]且f(x)≤g(x)成立,求
]且f(x)≤g(x)成立,求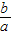 的取值范围.
的取值范围.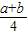 ,
,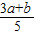 ]且f(x)≤g(x)成立,求
]且f(x)≤g(x)成立,求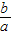 的取值范围.
的取值范围. 是正实数,设
是正实数,设 是奇函数
是奇函数 ,若对每个实数
,若对每个实数 ,
, 的元素不超过
的元素不超过 个,且存在
个,且存在 含有
含有