题目内容
x+y+z=1,则2x2+3y2+z2的最小值为( )
| A.1 | B.
| C.
| D.
|
证明:∵(2x2+3y2+z2)×(
+
+1 )≥(x+y+z)2=1,
∴2x2+3y2+z2≥1×
=
,
故 2x2+3y2+z2的最小值为
,
故选C.
| 1 |
| 2 |
| 1 |
| 3 |
∴2x2+3y2+z2≥1×
| 6 |
| 11 |
| 6 |
| 11 |
故 2x2+3y2+z2的最小值为
| 6 |
| 11 |
故选C.

练习册系列答案
相关题目
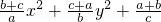 z2≥2(xy+yz+zx)
z2≥2(xy+yz+zx)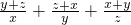 ≥2(
≥2(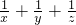 )
) x2+
x2+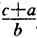 y2+
y2+ z2≥2(xy+yz+zx);
z2≥2(xy+yz+zx); ≥2(
≥2( )。
)。 z2≥2(xy+yz+zx)
z2≥2(xy+yz+zx) ≥2(
≥2( )
)