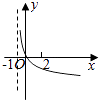题目内容
【题目】若函数![]() 在(0, 2π)内有两个不同零点
在(0, 2π)内有两个不同零点![]() 、
、![]() 。
。
(1)求实数![]() 的取值范围;
的取值范围;
(2)求![]() 的值。
的值。
【答案】(1)a的取值范围是(-2, -![]() )∪(-
)∪(-![]() , 2).
, 2).
(2)![]() .
.
【解析】
(1)由于![]() ,故可将问题转化为方程sin(x+
,故可将问题转化为方程sin(x+![]() 在(0, 2π)内有相异二解,由条件得到
在(0, 2π)内有相异二解,由条件得到![]() ,结合函数的图象可得所求范围.(2)根据
,结合函数的图象可得所求范围.(2)根据![]() 、
、![]() 为函数
为函数![]() 的零点可得sinα+
的零点可得sinα+![]() cosα+
cosα+![]() =0且sinβ+
=0且sinβ+![]() cosβ+
cosβ+![]() =0,将两式相减并结合和差化积公式可得tan
=0,将两式相减并结合和差化积公式可得tan![]() ,从而可得所求.
,从而可得所求.
(1)由题意得sinx+![]() cosx=2(
cosx=2(![]() sinx+
sinx+![]() cosx)=2 sin(x+
cosx)=2 sin(x+![]() ),
),
∵函数![]() 在(0, 2π)内有两个不同零点,
在(0, 2π)内有两个不同零点,
∴关于x的方程sinx+![]() cosx+a=0在(0, 2π)内有相异二解,
cosx+a=0在(0, 2π)内有相异二解,
∴方程sin![]() 在(0, 2π)内有相异二解.
在(0, 2π)内有相异二解.
∵0<![]() 2π,
2π,
∴![]() .
.
结合图象可得若方程有两个相异解,则满足![]() 且
且![]() ,
,
解得![]() 且
且![]() .
.
∴实数![]() 的取值范围是
的取值范围是![]() .
.
(2) ∵ ![]() 是方程的相异解,
是方程的相异解,
∴ sinα+![]() cosα+
cosα+![]() =0 ①
=0 ①
sinβ+![]() cosβ+
cosβ+![]() =0 ②
=0 ②
①![]() ②得(sinα
②得(sinα![]() sinβ)+
sinβ)+![]() ( cosα
( cosα![]() cosβ)=0,
cosβ)=0,
∴ 2sin![]() cos
cos![]() 2
2![]() sin
sin![]() sin
sin![]() ,
,
又sin![]() ≠0,
≠0,
∴ tan![]() ,
,
∴ 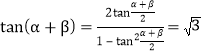 .
.

练习册系列答案
相关题目