题目内容
PA,PB是圆(x-a)2+(y-b)2=r2的两条切线,A,B为切点,∠APB=90°,则点P的轨迹方程为
(x-a)2+(y-b)2=2r2
(x-a)2+(y-b)2=2r2
.分析:设圆心为C,连结AC、BC、PC,由圆的切线的性质得到四边形PACB是边长等于半径r的正方形,其对角线|PC|=
r,因此点P的轨迹是以C为圆心、半径等于
r的圆,可得点P的轨迹方程.
| 2 |
| 2 |
解答:解:设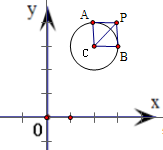 圆心为C(a,b),连结AC、BC、PC
圆心为C(a,b),连结AC、BC、PC
∵PA、PB分别与圆C相切,∠APB=90°,
∴四边形PACB是边长等于半径r的正方形,可得对角线|PC|=
r,
因此,动点P满足到定点C的距离等于定长
r,
其轨迹是以C为圆心、半径等于
r的圆
轨迹方程为(x-a)2+(y-b)2=2r2
故答案为:(x-a)2+(y-b)2=2r2
 圆心为C(a,b),连结AC、BC、PC
圆心为C(a,b),连结AC、BC、PC∵PA、PB分别与圆C相切,∠APB=90°,
∴四边形PACB是边长等于半径r的正方形,可得对角线|PC|=
| 2 |
因此,动点P满足到定点C的距离等于定长
| 2 |
其轨迹是以C为圆心、半径等于
| 2 |
轨迹方程为(x-a)2+(y-b)2=2r2
故答案为:(x-a)2+(y-b)2=2r2
点评:本题在圆中给出两条切线互相垂直,求它们的交点P的轨迹方程.着重考查了圆的性质、圆的标准方程和动点轨迹的求法等知识,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目