题目内容
(1)已知a+a－1=5，求a2+a－2，
，
； (2)已知a2x=
+1，求
.
解:(1)由a+a－1=5得(a+a－1)2=25.
∴a2+a－2=23.
∵>0,
又()2=a+a－1+2=7，
∴=
.
由(
)2=a+a－1－2=3,
∴=±
.
(2)
=
=
=
=
=2
－1,
或原式=a2x+a－2x－1=(
+1)+(
－1)－1=2
－1.
点评:本例解法是采用的整体代入的思想方法，如将a+a－1=5看作a的方程解出a=
，代入求值，则运算过程较为繁琐.
练习册系列答案
名校课堂系列答案
相关题目
，且n≥2)，现随意从A箱中取出3个球放入B箱，将B箱中的球充分搅匀后，再从中随意取出3个球放入A箱，则红球由A箱移入到B箱，再返回到A箱中的概率等于
选择题：
(1)
已知
，
，
，则
[
]|
(A)A 、B、D三点共线 |
(B)A 、B、C三点共线 |
|
(C)B 、C、D三点共线 |
(D)A 、C、D三点共线 |
(2)
已知正方形ABCD的边长为1，
，
，
，则
等于
[
]|
(A)0 |
(B)3 |
(C) |
(D) |
(3)
已知
，
，
，
，且四边形ABCD为平行四边形，则
[
]|
(A)a ＋b＋c＋d＝0 |
(B)a －b＋c－d＝0 |
|
(C)a ＋b－c－d＝0 |
(D)a －b－c＋d＝0 |
(4)
已知D、E、F分别是△ABC的边BC、CA、AB的中点，且
，
，
，则①
；②
；③
；④
中正确的等式的个数为
[
]|
(A)1 |
(B)2 |
(C)3 |
(D)4 |
(5)
若
，
是夹角为60°的两个单位向量，则
；
的夹角为
[
]|
(A)30° |
(B)60° |
(C)120° |
(D)150° |
(6)
若向量a、b、c两两所成的角相等，且
，
，
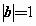，则
等于
[
]|
(A)2 |
(B)5 |
(C)2 或5 |
(D)  |
(7)
等边三角形ABC的边长为1，
，
，
，那么a·b＋b·c＋c·a等于
[
]|
(A)3 |
(B) －3 |
(C) |
(D) |
