题目内容
偶函数f(x)满足f(x-2)=f(x+2),且在x∈[0,2]时,f(x)=2cos
x则关于x的方程f(x)=(
)x在 x∈[-2,6]上解的个数是
| π |
| 4 |
| 1 |
| 2 |
4
4
.分析:根据题意,函数f(x)是周期为4的是偶函数,在[0,2]上的表达式为f(x)=2cos
x,由此不难作出f(x)在[-2,6]上的图象,再在同一坐标系内作出函数y=(
)x的图象,观察两个图象的交点个数,即得本题方程实数根的个数.
| π |
| 4 |
| 1 |
| 2 |
解答: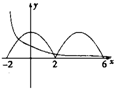 解:∵当x∈[0,2]时,0≤
解:∵当x∈[0,2]时,0≤
x≤
π,f(x)=2cos
x
∴函数f(x)在x=0时,函数值有最大值f(0)=2cos0=2,
在x=2时,函数值有最小值f(2)=2cos
π=0.
由此作出函数f(x)在x∈[0,2]时的图象,呈减函数趋势如图
∵函数f(x)是偶函数,
∴f(x)在[-2,0]上的图象与[0,2]上的图象关于y轴对称,如图所示
∵函数f(x)满足f(x-2)=f(x+2),∴函数f(x)是周期T=4的周期函数.
因此,将f(x)在[-2,2]上的图象向右平移一个周期,得f(x)在[2,6]上的图象
∴函数f(x)在[-2,6]上的图象如右图所示,是位于x轴上方的两段余弦型曲线弧
在同一坐标系内作出函数y=(
)x的图象,可得它经过点(0,1),呈减函数趋势如图
因为两个图象有4个交点,得关于x的方程f(x)=(
)x的实数根也有4个.
故答案为:4.
 解:∵当x∈[0,2]时,0≤
解:∵当x∈[0,2]时,0≤| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
∴函数f(x)在x=0时,函数值有最大值f(0)=2cos0=2,
在x=2时,函数值有最小值f(2)=2cos
| 1 |
| 2 |
由此作出函数f(x)在x∈[0,2]时的图象,呈减函数趋势如图
∵函数f(x)是偶函数,
∴f(x)在[-2,0]上的图象与[0,2]上的图象关于y轴对称,如图所示
∵函数f(x)满足f(x-2)=f(x+2),∴函数f(x)是周期T=4的周期函数.
因此,将f(x)在[-2,2]上的图象向右平移一个周期,得f(x)在[2,6]上的图象
∴函数f(x)在[-2,6]上的图象如右图所示,是位于x轴上方的两段余弦型曲线弧
在同一坐标系内作出函数y=(
| 1 |
| 2 |
因为两个图象有4个交点,得关于x的方程f(x)=(
| 1 |
| 2 |
故答案为:4.
点评:本题以一个关于x的方程根的个数讨论为载体,考查了函数的单调性与奇偶性、基本初等函数图象作法和函数的周期等知识点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0.则( )
| f(x2)-f(x1) |
| x2-x1 |
| A、f(3)<f(-2)<f(1) |
| B、f(1)<f(-2)<f(3) |
| C、f(-2)<f(1)<f(3) |
| D、f(3)<f(1)<f(-2) |
定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上单调递增,a=f(3),b=f(
),c=f(2),则a,b,c大小关系是( )
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、b>c>a |
| D、c>b>a |