题目内容
已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,记an与an+1的等差中项为kn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若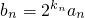 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(Ⅲ)设集合 ,等差数列{cn}的任意一项cn∈A∩B,其中c1是A∩B中的最小数,且110<c10<115,求{cn}的通项公式.
,等差数列{cn}的任意一项cn∈A∩B,其中c1是A∩B中的最小数,且110<c10<115,求{cn}的通项公式.
解:(I)∵点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,∴ ,
,
当n≥2时,an=Sn-Sn-1=2n+1.…(2分)
当n=1时,a1=S1=3满足上式,
所以数列{an}的通项公式为an=2n+1.…(3分)
(II)∵kn为an与an+1的等差中项
∴ …(4分)
…(4分)
∴ .
.
∴ ①
①
由①×4,得 ②
②
①-②得: =
=
∴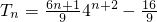 …(8分)
…(8分)
(III)∵
∴A∩B=B
∵cn∈A∩B,c1是A∩B中的最小数,∴c1=6.
∵{cn}是公差为4的倍数的等差数列,∴ .…(10分)
.…(10分)
又∵110<c10<115,∴ ,解得m=27.
,解得m=27.
所以c10=114,
设等差数列的公差为d,则 ,…(12分)
,…(12分)
∴cn=6+(n+1)×12=12n-6,
∴cn=12n-6.…(13分)
分析:(I)根据点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,可得 ,再写一式,两式相减,即可求得数列{an}的通项公式;
,再写一式,两式相减,即可求得数列{an}的通项公式;
(II)先确定数列的通项,再利用错位相减法求数列的和;
(III)先确定A∩B=B,再确定{cn}是公差为4的倍数的等差数列,利用110<c10<115,可得c10=114,由此可得{cn}的通项公式.
点评:本题考查数列与函数的关系,考查数列的通项与求和,正确运用求和公式是关键.
 ,
,当n≥2时,an=Sn-Sn-1=2n+1.…(2分)
当n=1时,a1=S1=3满足上式,
所以数列{an}的通项公式为an=2n+1.…(3分)
(II)∵kn为an与an+1的等差中项
∴
 …(4分)
…(4分)∴
 .
.∴
 ①
①由①×4,得
 ②
②①-②得:
 =
=
∴
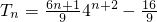 …(8分)
…(8分)(III)∵

∴A∩B=B
∵cn∈A∩B,c1是A∩B中的最小数,∴c1=6.
∵{cn}是公差为4的倍数的等差数列,∴
 .…(10分)
.…(10分)又∵110<c10<115,∴
 ,解得m=27.
,解得m=27.所以c10=114,
设等差数列的公差为d,则
 ,…(12分)
,…(12分)∴cn=6+(n+1)×12=12n-6,
∴cn=12n-6.…(13分)
分析:(I)根据点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,可得
 ,再写一式,两式相减,即可求得数列{an}的通项公式;
,再写一式,两式相减,即可求得数列{an}的通项公式;(II)先确定数列的通项,再利用错位相减法求数列的和;
(III)先确定A∩B=B,再确定{cn}是公差为4的倍数的等差数列,利用110<c10<115,可得c10=114,由此可得{cn}的通项公式.
点评:本题考查数列与函数的关系,考查数列的通项与求和,正确运用求和公式是关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |