题目内容
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是

- A.点H是△A1BD的垂心
- B.AH垂直平面CB1D1
- C.AH的延长线经过点C1
- D.直线AH和BB1所成角为45°
D
分析:如上图,正方体的体对角线AC1有以下性质:
①AC1⊥平面A1BD,AC1⊥平面CB1D1;②AC1被平面A1BD与平面CB1D1三等分;③AC1= AB等.
AB等.
(注:对正方体要视为一种基本图形来看待.)
解答:因为三棱锥A-A1BD是正三棱锥,所以顶点A在底面的射影H是底面中心,所以选项A正确;
易证面A1BD∥面CB1D1,而AH垂直平面A1BD,所以AH垂直平面CB1D1,所以选项B正确;
连接正方体的体对角线AC1,则它在各面上的射影分别垂直于BD、A1B、A1D等,所以AC1⊥平面A1BD,则直线A1C与AH重合,所以选项C正确;
故选D.
点评:本题主要考查正方体体对角线的性质.
分析:如上图,正方体的体对角线AC1有以下性质:
①AC1⊥平面A1BD,AC1⊥平面CB1D1;②AC1被平面A1BD与平面CB1D1三等分;③AC1=
 AB等.
AB等.(注:对正方体要视为一种基本图形来看待.)
解答:因为三棱锥A-A1BD是正三棱锥,所以顶点A在底面的射影H是底面中心,所以选项A正确;
易证面A1BD∥面CB1D1,而AH垂直平面A1BD,所以AH垂直平面CB1D1,所以选项B正确;
连接正方体的体对角线AC1,则它在各面上的射影分别垂直于BD、A1B、A1D等,所以AC1⊥平面A1BD,则直线A1C与AH重合,所以选项C正确;
故选D.
点评:本题主要考查正方体体对角线的性质.

练习册系列答案
相关题目
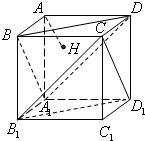 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题:
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题: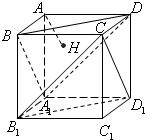
 (2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( )
(2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( )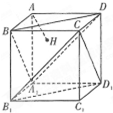 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )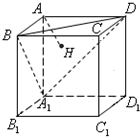 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则点H到平面A1B1C1D1 的距离为
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则点H到平面A1B1C1D1 的距离为