题目内容
（本小题满分12分）
已知函数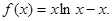
（I）求函数
处的切线的方程；
（II）设实数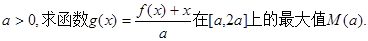
【答案】
解：（Ⅰ）函数
的定义域是
，
∴
， ………………1分
，
，切点为(e，0) ，………………3分
∴在
处的切线的方程为
。 ………………4分
（Ⅱ）
，
，
令
得
，
知函数
在
上单调递减；在
上单调递增。………………6分
∵
，
，
⑴当
，即
，函数
在
上单调递增，则
；
………………7分
⑵当
，即
，函数在上单调递减，则
；
………………8分
⑶当
，即
，函数在
上单调递减，在
上单调递增，
，
①当
，
，
，则； …………9分
②当
，
，
，则；………………10分
③当
，
，
，则
。………………11分
综上，函数在上的最大值
。………………12分
【解析】略
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
