Question

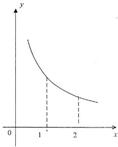已知函数f（x）在区间（0，+∞）上的图象如图所示，记为K₁=f′（1），K₂=f′（2），K₃=f（2）-f（1），则K₁，K₂，K₃之间的大小关系为

1. A.
   K₁＜K₂＜K₃
2. B.
   K₃＜K₂＜K₁
3. C.
   K₁＜K₃＜K₂
4. D.
   K₂＜K₃＜K₁

Answer 1

A
分析：分析f（x）在区间（0，+∞）上的图象，从左到右下降的坡度越来越小，说明其导函数的函数值为负，且随着自变量x值的增大而增大．故不难分析出K₁，K₂，K₃之间的大小关系．
解答：分析f（x）在区间（0，+∞）上的图象，
从左到右下降的坡度越来越小，
说明其导函数的函数值为负，
且随着自变量x值的增大而增大．
∴K₁＜K₂＜0
K₃=f（2）-f（1）=K₂-K₁＞0，
故K₁＜K₂＜K₃
故答案选A
点评：f（x）的图象，从左到右下降的坡度越来越小，说明其导函数的函数值为负，且随着自变量x值的增大而增大．
f（x）的图象，从左到右下降的坡度越来越大，说明其导函数的函数值为负，且随着自变量x值的增大而减小．
f（x）的图象，从左到右上升的坡度越来越小，说明其导函数的函数值为正，且随着自变量x值的增大而减小．
f（x）的图象，从左到右上升的坡度越来越大，说明其导函数的函数值为正，且随着自变量x值的增大而增大．